
이번 포스팅에서는 비지도 학습의 대표적인 clustering 알고리즘인 K-Means clustering에 대해 알아보도록 하겠습니다.
들어가기에 앞서 비지도 학습(unsupervised learning)에 대해 알 필요가 있습니다.
해당 포스트의 초반 부분을 참고해주세요!
https://sanmldl.tistory.com/9?category=976947
데이터 전처리 with python (1)
이번 포스트에서는 파이썬을 활용하여 데이터 전처리 하는 방식에 대해 혼공머신 예제를 통해 알아보도록 하겠습니다. 1. 지도학습(supervised learning)이란? 들어가기에 앞서, 지도학습(supervised learn
sanmldl.tistory.com
간략하게 말하면, 비지도학습은 지도학습과는 다르게 정답 레이블이 없이 주어진 데이터를 통해 학습을 진행하는 형식입니다.
가령 생선의 몸무게와 넓이 데이터에 맞는 정답 즉 빙어, 도미을 할당해주고 구분하는 것이 지도학습이라면,
정답 데이터 없이 생선의 몸무게와 넓이 데이터만으로 구분하는 것이 비지도학습입니다.
비지도학습에는 데이터를 군집화하거나 연관 규칙을 찾는 데 주로 사용됩니다.
군집화는 지도학습의 classification(분류)와 엄연히 다르다는 것을 알아야합니다.
실생활에서 사용되는 군집화의 예시는 추천 엔진 알고리즘, 검색한 것과 관련된 결과(검색 엔진), 고객 세분화 등이 있습니다.
군집화는 비지도 학습으로 정답 없이 데이터의 유사도를 비교하여 비슷한 그룹끼리 묶어주는 것을 의미합니다.
대표적인 군집화 알고리즘으로 K-Means 알고리즘이 있습니다.
K-Means 알고리즘은 다음과 같이 이뤄집니다.

1. 초기에 k개의 중심점을 임의로 정합니다.
2. 중심점에 가까운 데이터를 구분지어 clustering합니다.
3. 해당 cluster안에 있는 데이터들의 중심으로 중심점을 갱신합니다.
4. 중심점의 갱신이 더 이상 이뤄지지 않을 때까지 2,3단계를 반복합니다.
결국 K-Means도 데이터의 유사도(ex.유클리디안 거리,맨하탄 거리)를 바탕으로 중심점과 가까운 데이터를 그룹화하는 것입니다.
그렇다면 K-Means는 "몇 개의 그룹으로 나눌 것인가?(k개의 그룹)" / "데이터와 중심점과의 평균 거리를 최소화 하는 알고리즘" 이구나!
라는 것을 직관적으로 알 수 있습니다.
K-Means의 장점은 매우 직관적이며 구현하기 쉽다는 것입니다.
단점으로는 데이터의 분산 구조를 반영하지 않으며, 이상 값에 대해서도 반영이 이뤄지며, 적절한 k값을 정해주어야 한다는 것입니다.
혼공머신 책에서 제공하는 데이터를 바탕으로 k-means 학습 과정을 구현해보겠습니다.
해당 데이터는 (300,100,100)의 크기를 가지는 사과, 파인애플, 바나나의 이미지 데이터입니다.
#파일 업로드
!wget http://bit.ly/fruits_300_data -o fruits_300.npywget 명령어를 사용하여 데이터를 불러옵니다. 코랩에는 wget이 이미 설치되어있으므로 코랩 환경에서 실행하는 것을 추천드립니다.
import numpy as np
from sklearn.cluster import KMeans
fruits = np.load('fruits_300_data')
fruits_2d = fruits.reshape(-1,100*100)
#3개의 그룹으로 나눔
km = KMeans(n_clusters=3, random_state = 42)
km.fit(fruits_2d)
print(np.unique(km.labels_, return_counts = True))해당 데이터는 .npy파일 형식이기 때문에 np.load로 로드해줍니다.
데이터는 (300,100,100)으로 구성되어 있습니다. 100*100 size의 이미지가 300개 있다는 의미입니다.
학습을 위해 100*100을 1차원 벡터로 만들어줍니다.
reshape(-1, 100*100)을 하면 100*100(10000)의 크기로 각 이미지별 픽셀 값을 1차원 벡터로 표현할 수 있습니다.
-1을 앞에 붙이면 자동으로 남은 차원으로 할당해줍니다. (300,100*100)과 같은 의미입니다.
k를 3으로 하는(3개의 그룹을 만드는) 모델을 만들어주고 데이터를 학습시켜줍니다.
이 때, 비지도학습이므로 정답 레이블이 없기 때문에 fruits_2d만 입력해도 학습이 이뤄집니다.
학습이 이뤄지면 labels_속성에 각 cluster 값에 대해 숫자로 표현됩니다.
여기서 저희가 k를 3으로 설정했기 때문에 0,1,2(3개의 cluster)로 표현될 것 입니다.
마지막 줄에서 각 cluster별로 몇 개의 이미지가 있는지 알 수 있습니다.
학습이 잘 이루어졌는지 시각적으로 확인해보겠습니다.
코드는 다음과 같습니다.
import matplotlib.pyplot as plt
#시각화를 위한 함수 선언
def draw_fruits(arr, ratio =1):
n = len(arr)
rows = int(np.ceil(n/10))
cols = n if rows < 2 else 10
fig, axs = plt.subplots(rows, cols, figsize =(cols * ratio, rows * ratio), squeeze = False)
for i in range(rows):
for j in range(cols):
if i * 10 + j < n:
axs[i,j].imshow(arr[i*10+j], cmap = 'gray_r')
axs[i,j].axis('off')
plt.show()시각화를 위한 함수를 선언하여 반복해서 사용하기 용이하게 했습니다.
불리안 인덱싱을 통해 cluster가 1인 이미지를 확인해보겠습니다.
draw_fruits(fruits[km.labels_ == 1])fruits 데이터에서 km.labels_가 1인 데이터에 대해 반환이 이뤄집니다.
즉, k-means알고리즘으로 학습한 1 cluster가 무엇인지 이미지 사진으로 보여주는 것입니다.
코드를 실행하면 다음과 같이 1 cluster는 바나나 cluster입니다. km.labels_ == 0 , km.labels_ ==2 로 바꿔
(불리언 인덱싱을 다르게 하여) 달라지는 결과값들을 확인해보세요!

- 적합한 k구하기(적절한 클러스터 개수 정하기 = 몇 개의 그룹으로 나눌까?)
적절한 k를 구하는 것은 k-means알고리즘에서 필수적인 요소중 하나입니다.
그렇다면 적절한 k를 어떻게 구할 수 있을까요?
직관적으로 파악하려면 데이터를 시각화 하여(ex. 산점도) 데이터가 분산된 정도를 보고 k를 정할 수 있습니다.
하지만 보다 정확하고 논리적으로 k를 구하기 위해서는 다른 방식이 더 효과적입니다.
적절한 k를 구하기 위한 완벽한 방법은 없지만 대표적인 방법인 elbow 방법에 대해 알아보겠습니다.
-Elbow point를 찾아라!
적절한 k를 찾기 위한 Elbow 방법은 결국 elbow point를 찾는 것입니다.
elbow point를 알아내기 위해서는 inertia라는 값을 알 필요가 있습니다.
Inertia(이너셔)란 클러스터 중심점(centroid)와 클러스터에 속한 샘플들의 거리의 제곱 합을 나타냅니다.
제곱을 해줌으로써 거리가 상쇄되는 것을 막아주면서 각 클러스터에 샘플들이 얼마나 조밀조밀하게 집합되어 있는지
알려주는 것 입니다. 즉 얼마나 가깝게 모여있는지 나타내는 값으로 판단할 수 있습니다.
일반적으로 클러스터 개수가 늘어나면 이너셔의 값도 줄어들 것입니다.
클러스터가 늘어나면 각각의 클러스터 크기가 줄어들면서 클러스터에 할당된 샘플들이 보다 오밀조밀하게 모여있을 것입니다.
이에 착안하여 elbow방법은 클러스터 개수를 늘려가면서 이너셔를 관찰합니다.
클러스터 개수가 늘면서 이너셔는 감소하겠지만 감소하는 정도가 꺾이는 포인트가 있습니다.
이 포인트를 elbow point라고 하며 이 때의 클러스터 개수가 k값이 되는 것 입니다.
이전 코드에서 활용했던 데이터로 예시를 들어보겠습니다.
코드는 다음과 같습니다.
#k별 이너셔를 관찰하기 위한 빈 리스트 생성
inertia = []
#k를 2~6까지의 값으로 두고 관찰
for k in range(2,7):
km = KMeans(n_clusters = k, random_state = 42)
km.fit(fruits_2)
inertia.append(km.inertia_)
#Elbow point찾기(시각화)
plt.plot(range(2,7), inertia)
plt.xlabel('k')
plt.ylabel('elbow point')
plt.show()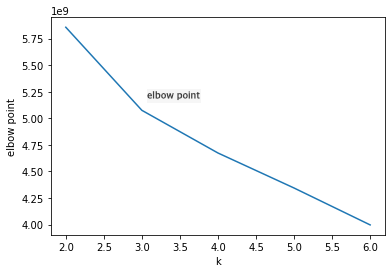
k-means 모델의 inertia_속성에는 모델이 학습하여 만든 클러스터의 inertia값이 저장되어 있습니다. 이를 활용하여
k가 증가함에 따라 inertia값이 변하는 것을 시각화하여 관찰하면 됩니다.
K가 3일 때 이너셔가 감소하는 속도가 확 줄어듭니다. 이때 가장 효율적으로 클러스터 개수를 정했다고 할 수 있겠네요!
elbow point 즉 사람의 팔꿈치와 같은 모양을 하고 있어 elbow point라고 합니다.
적합한 k를 구했는지 확인하는 즉, k-means clustering이 데이터로부터 잘 학습하여 잘 나눠주었는지 판단하는 지표로는
Dunn index, silhouette 계수를 확인하는 것입니다.
이에 대한 내용은 다음 포스팅에서 알아보도록 하겠습니다.
이번 포스팅에서는 비지도 학습과 그 중 k-means clustering에 대해 공부했으며,
최적의 k를 구하는 방법에 대해서도 알아보았습니다.
'Book Review > [혼공머신] 리뷰' 카테고리의 다른 글
| 순환 신경망(RNN)의 개념 (1) | 2023.05.10 |
|---|---|
| GBM기반 앙상블: XGboost, LightGBM (0) | 2023.01.16 |
| 트리 앙상블 (1) | 2023.01.16 |
| 트리 알고리즘: 결정 트리 (0) | 2023.01.10 |
| 확률적 경사 하강법 (2) | 2023.01.04 |