
이전 포스트에서 손실 함수에 대한 그레이디언트를 계산하여 손실 함수가 최소가 되는 지점을 찾는 방식을 배웠습니다.
그렇다면 수 천, 수 만개로 이루어진 모델 파라미터의 그레이디언트를 실제로 어떻게 계산할 수 있을까요?
바로 역전파 알고리즘(backpropagation) 덕분 입니다.
이번 포스팅에서는 역전파 알고리즘에 대해 공부하여 리뷰해보겠습니다.
역전파는 순전파(forward propagation)의 반대 개념입니다.
순전파는 입력 데이터가 은닉층을 따라 출력층으로 나오는 추론 과정을 의미합니다.

그림1의 화살표 방향을 확인해보면 순전파 알고리즘을 파악할 수 있습니다.
개념적으로 순전파 알고리즘의 진행방향을 반대로 바꾸면 역전파 알고리즘이 됩니다.
역전파를 사용하는 이유는 입력층에서 출력층 값이 도출되고 그 값의 손실 함수까지 도달하는 모든 계산 식들이 대부분 미분 가능하기 때문입니다. 즉, 순전파의 연산에서 관여한 파라미터의 미세한 변화가 얼마나 손실 함수 값의 증감에 기여했는 지를 보는 것 입니다.
역전파 계산을 이해하기 위해 먼저, 2개의 층으로 구성된 모델의 순전파 계산을 살펴보겠습니다.

그림2를 보면 입력과 w1, b1이 계산되어 relu함수를 통해 빠져나오면, 그 값이 다시 w2, b2와 계산되어 softmax함수를 통해
빠져나온 값을 가지게 됩니다.
이전 포스트에서 계속해서 봐왔던 방식 입니다.
순전파 예시를 보았으니 역전파가 이뤄지는 계산과정의 예를 들어 보겠습니다.
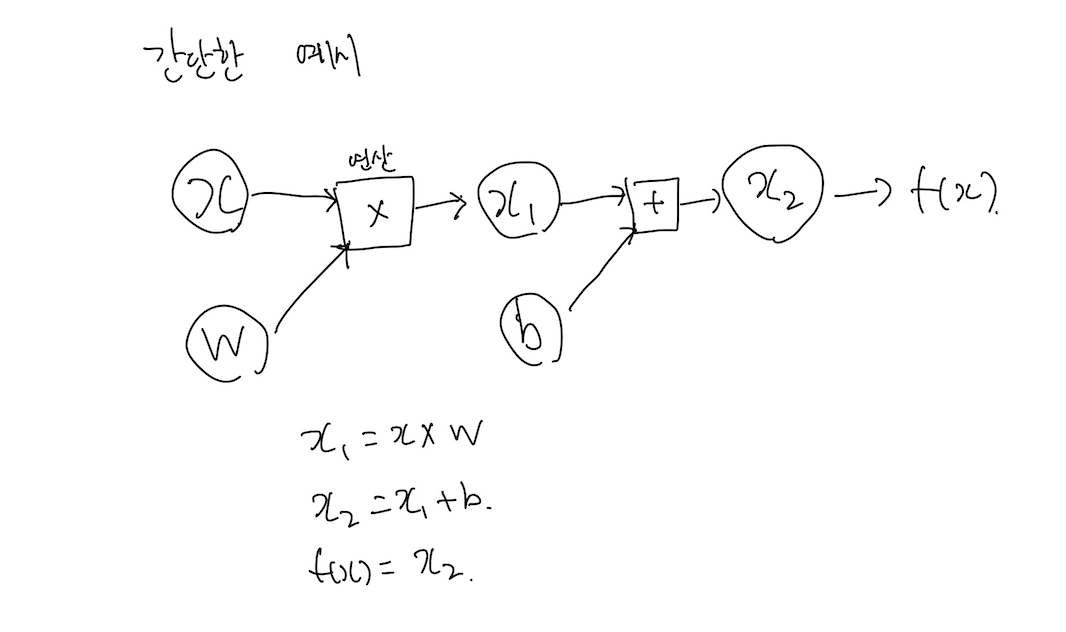
f(x)라는 값에 도달하는 순전파의 간단한 예시입니다.
각 연산은 + 와 x로 구성되어 있습니다.
이제 각각의 입력노드에 구체적인 값을 넣어보겠습니다.

그림3의 각 입력노드 x=2, w=3, b=1을 넣었습니다.
순전파 알고리즘에 따르면 그림4와 같습니다.

반면 역전파 알고리즘에 따르면 그림5와 같습니다.
계산할 때 순전파와 달리 초록색 선을 따라가며 계산 방향을 따라가주시면 됩니다.
f(x)에서 x로 가는 방향에서 각각의 x가 바뀔 때 f(x)가 얼마나 바뀌는지 확인하는 것이 역전파 알고리즘입니다.
따라서 역전파 방향의 선에 각 값들의 기울기를 구해줍니다(미분).
차례대로 계산을 해보겠습니다.
(1) x2에 대하여 f(x)를 미분하면 1이 나옵니다. f(x) = x2 -> f(x)' = 1
(2) x1에 대하여 x2를 미분하면 1이 나옵니다. x2 = x1 + b -> x2' = 1
(3) x에 대하여 x1을 미분하면 w가 나옵니다. x1 = x * w -> x1' = 1*w = w
다른 노드에 대해서도 적용을 하면 역전파 계산에 의해 각 노드에서 파란색 동그라미 값들이 나옵니다.
앞서 본 값(x = 2, w = 3, b = 1)을 대입하면 역전파 계산에 의해 x에 대한 f(x)의 미분한 값은 3( w=3 )이 나옵니다.
역전파 알고리즘에서 입력으로 들어온 f(x)의 변화에 x가 기여한 정도를 알 수 있게 된 것 입니다.
이러한 계산이 가능하게 하는 것은 바로 연쇄법칙(chain rule) 때문입니다.
각 식에 대한 도함수를 알고 있으면 그 다음 식의 도함수를 계산할 수 있게 해줍니다.
식으로 표현하면 마치 사슬처럼 보이기 때문에 연쇄법칙이라고 합니다.
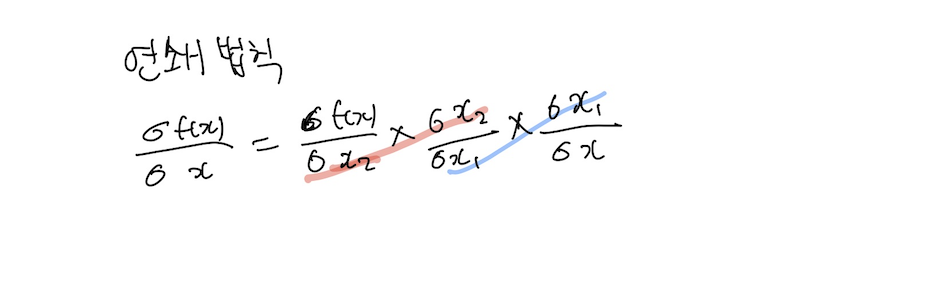
그림6에서는 앞서 본 예시로 연쇄법칙을 적용한 과정입니다.
역전파 순서에 맞게 도함수를 구하고 다음 도함수를 구하고 ...반복하면 결국 빨간선, 파란선 처럼 생략할 수 있습니다.
눈치가 빠른 분들은 이미 눈치 채셨겠지만
+연산의 역전파에서는 1이 흘러 들어오고 x연산의 역전파는 서로 다른 노드의 값이 흘러 들어옵니다.
간단한 예시를 통해 역전파 알고리즘의 계산 방식을 알아보았습니다.
물론 실제 딥러닝의 역전파 과정에서는 더욱 복잡한 연산이 이뤄지고 그것을 역전파 계산을 해야하기 때문에 구하기 어렵습니다.
보다 자세한 내용을 공부하고 싶으신 분들을 위해 역전파 알고리즘에 대한 참고 영상 링크를 올리도록 하겠습니다.
'Book Review > [케라스 창시자에게 배우는 딥러닝] 리뷰' 카테고리의 다른 글
| 신경망을 이용한 이진 분류: 영화 리뷰 분류 (2) | 2022.12.28 |
|---|---|
| 텐서플로우를 통한 딥러닝 모델 직접 구현 (0) | 2022.12.07 |
| keras API를 통한 간단한 딥러닝 모델 만들기 (0) | 2022.12.05 |
| 신경망 이해를 위한 Tensor(텐서), Gradient(그레이디언트) (1) | 2022.11.23 |
| 딥러닝이란 ? (1) | 2022.11.17 |