cs231n은 stanford univ에서 제공하는 neural network(NN), convolution neural network(CNN) 관련 deep learning 강좌다.
이를 공부해 보고 정리해보고자 한다!
1장에서는 이 강좌에 대한 introduction part이다. 이 부분에서 컴퓨터 비전의 역사와 발전 양상을 다루고 있다.
내용이 궁금한 사람은 아래의 링크에서 직접 보는 것을 추천한다.
https://www.youtube.com/watch?v=vT1JzLTH4G4&list=PLC1qU-LWwrF64f4QKQT-Vg5Wr4qEE1Zxk
2장은 computer vision task 중 가장 고전적이면서 근본적인 image classification를 다룬다.
이 task에서 고려해야 할 한계점이 무엇이며 이를 해결하기 위해 어떤 접근법이 등장했는지 알아보자.
image data는 semantic gap이라는 문제점을 가지고 있다.
semantic gap을 직역하면 의미적 차이 정도로 볼 수 있는데,
말 그대로 사람이 인식하여 받아들이는 것과 컴퓨터가 인식하여 받아들이는 의미 간의 차이를 의미한다.
아래의 그림1을 보면 사람은 왼쪽의 그림은 고양이가 있다고 받아들인다.
하지만 컴퓨터는 2차원 배열(혹은 3차원)로 나열한 픽셀 값들로 받아들이게 된다.

컴퓨터 비전에서는 이러한 semantic gap로 인해 발생하는 challenge들이 생긴다.
1. Viewpoint variation: 시점에 따라 같은 객체여도 다른 픽셀 값으로 이뤄진다.
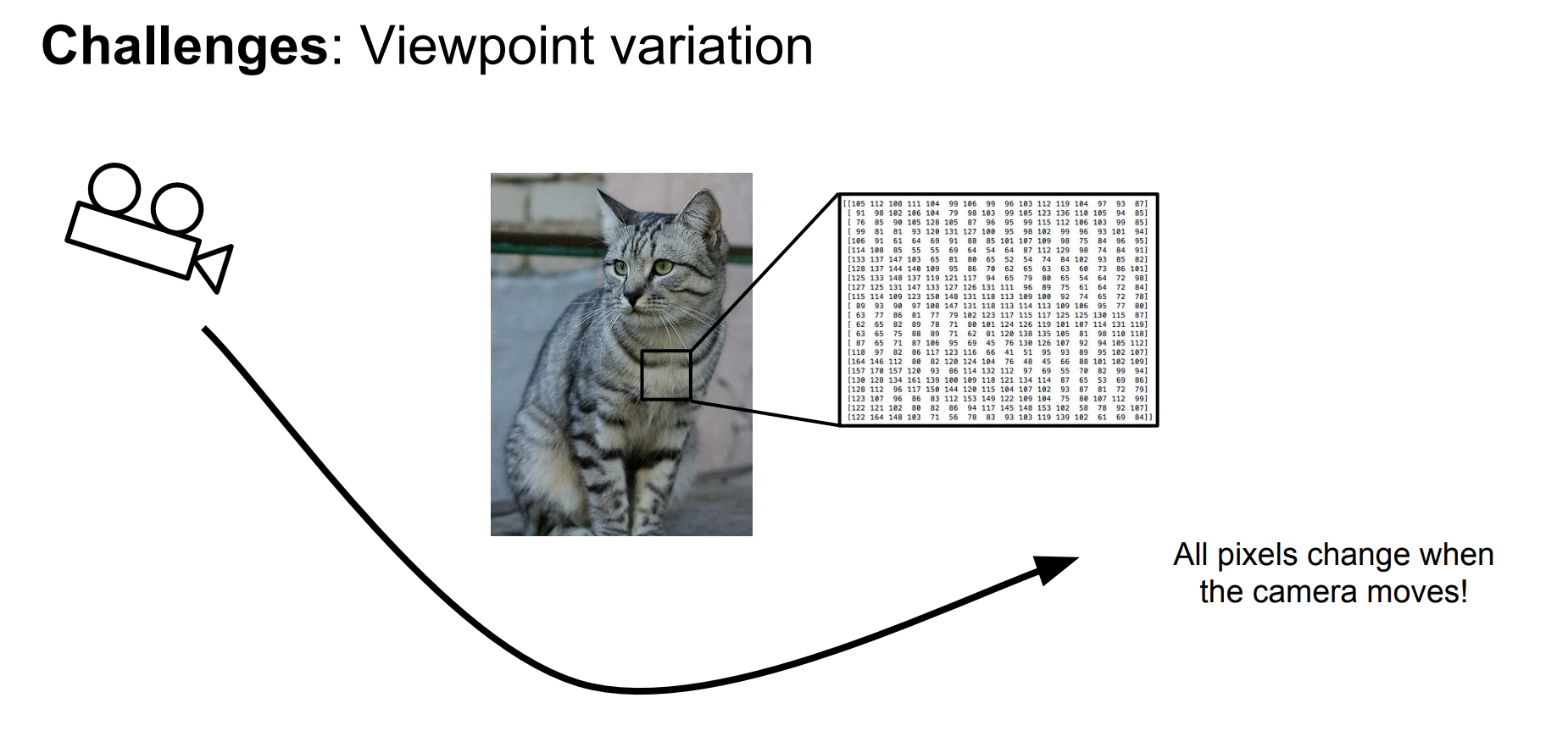
2. illumination: 같은 객체여도 조명에 따라 서로 다른 픽셀 값으로 이뤄진다.

3. Deformation: 같은 객체라도 형태에 따라 서로 다른 픽셀 값으로 이뤄진다.

4. Occlusion: 같은 객체라도 가려진 정도나 위치에 따라 픽셀 값이 달라진다.

5. Background clutter: 같은 객체라도 비슷한 배경과 구분되어지지 못한다.

6. Intraclass variation: intraclass(같은 객체)에 대하여 다른 객체로 구분한다.

즉, 이미지 데이터는 sematic gap으로 다양한 문제를 야기한다. 이를 고려하고자 하는 게 CV task의 핵심이다.
image classifier의 발전 양상을 통해 semantic gap의 다양한 문제를 어떻게 해결했는지 알아보자.
우선, 하드코딩 방식으로 알고리즘을 짜게 된다면 다양한 class를 분류하는 데 큰 어려움이 있을 것이다.
초창기에는 edge를 검출하여 corner를 찾고 이를 활용하여 분류하려는 접근법이 만연했다.
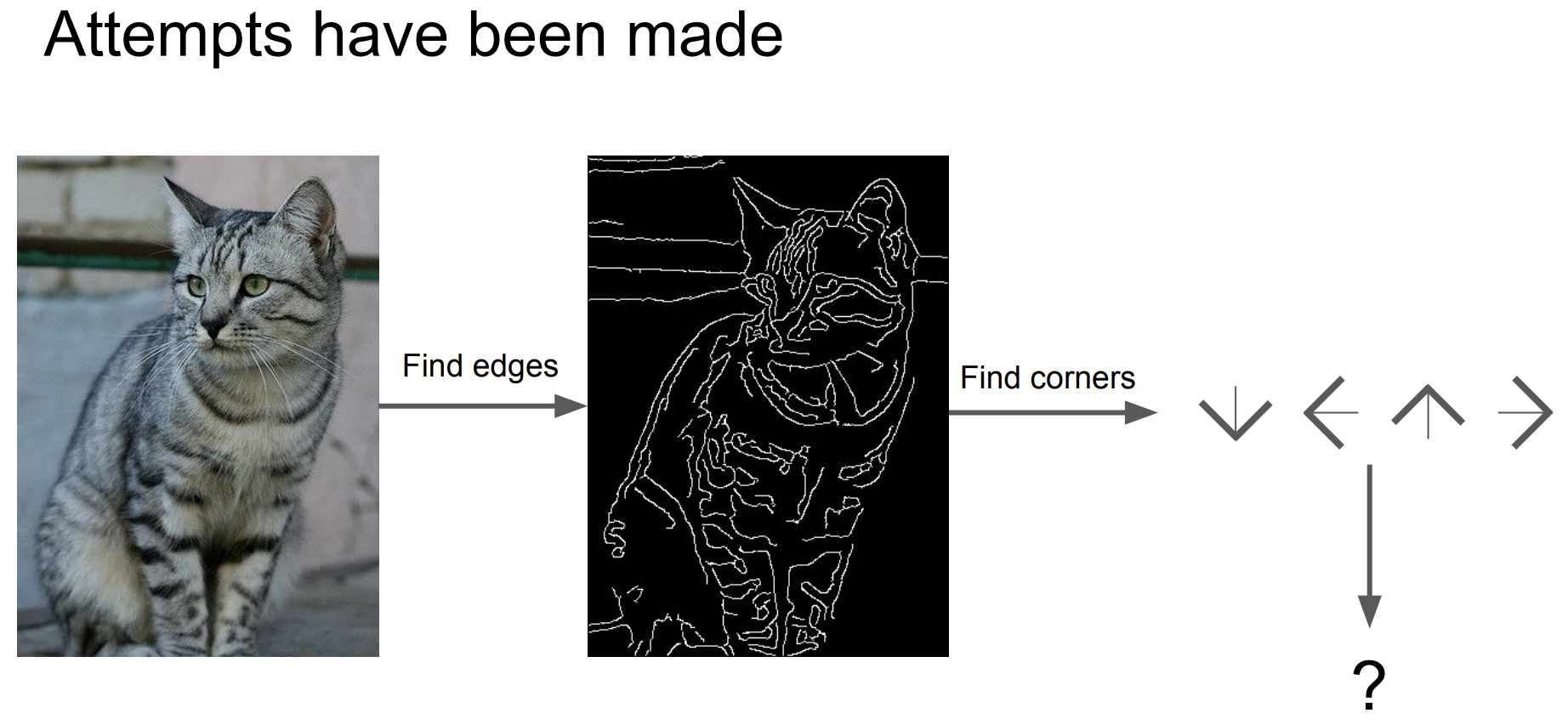
그러나 이 접근법은 앞서 말한 semantic gap의 문제점을 직접 고려하기 힘들다.
따라서 어떠한 통용되는 분류 알고리즘을 적용하는 것이 아니라 데이터 중심의 classifier를 만들어보자는 아이디어가 등장했다.

data-driven approach: dataset을 구축하여 머신러닝 classifier를 훈련시키고 새 image에 대해 분류해 보자!
처음 고려될 만한 접근법은 nearest neighbor(NN)이다.
NN의 방식은 다음과 같다.
train dataset의 이미지(5만개)와 test image 간 각각의 이미지에 대하여 거리를 구한다.
이때의 거리는 L1 distance로 절댓값의 차이다.
그렇게 구해진 pixel wise difference가 나오면 그 요소를 다 더하여 하나의 스칼라 값으로 만든다.
그러면 하나의 test image마다 50000개의 스칼라 값이 나오게 된다. 그중 가장 작은 값의 label로 할당한다.
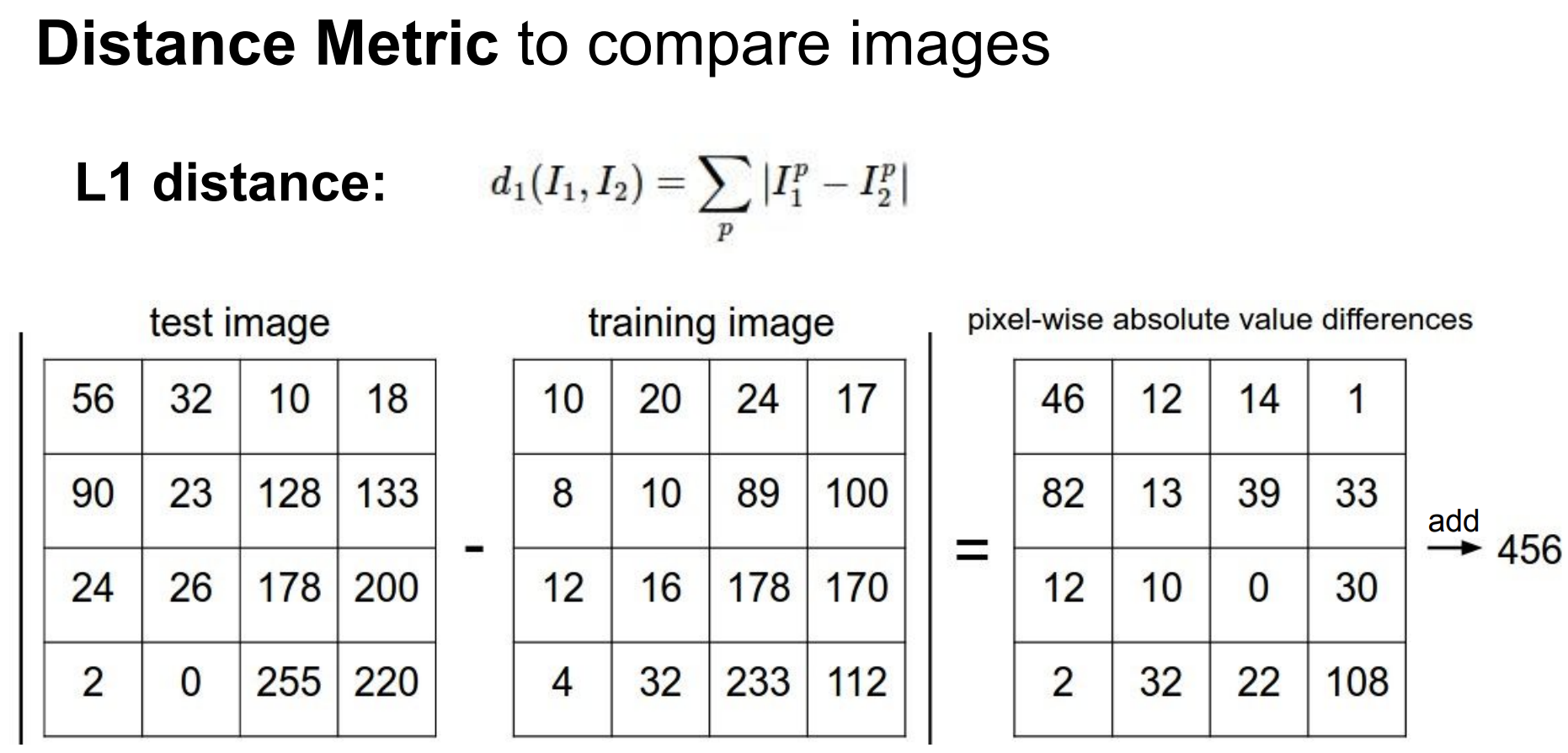
이 접근법은 data-driven이라는 점에서는 긍정적이지만 N개의 sample을 학습시키고 분류하는데
train에서는 O(1)(단순 저장), predict에는 O(N)(n개 스칼라값 계산)의 시간복잡도를 가진다는 점에서 단점이 있다.
그 이유는 train에서는 느릴지라도 test(predict)시에는 더 빠른 classifier가 필요하기 때문이다.
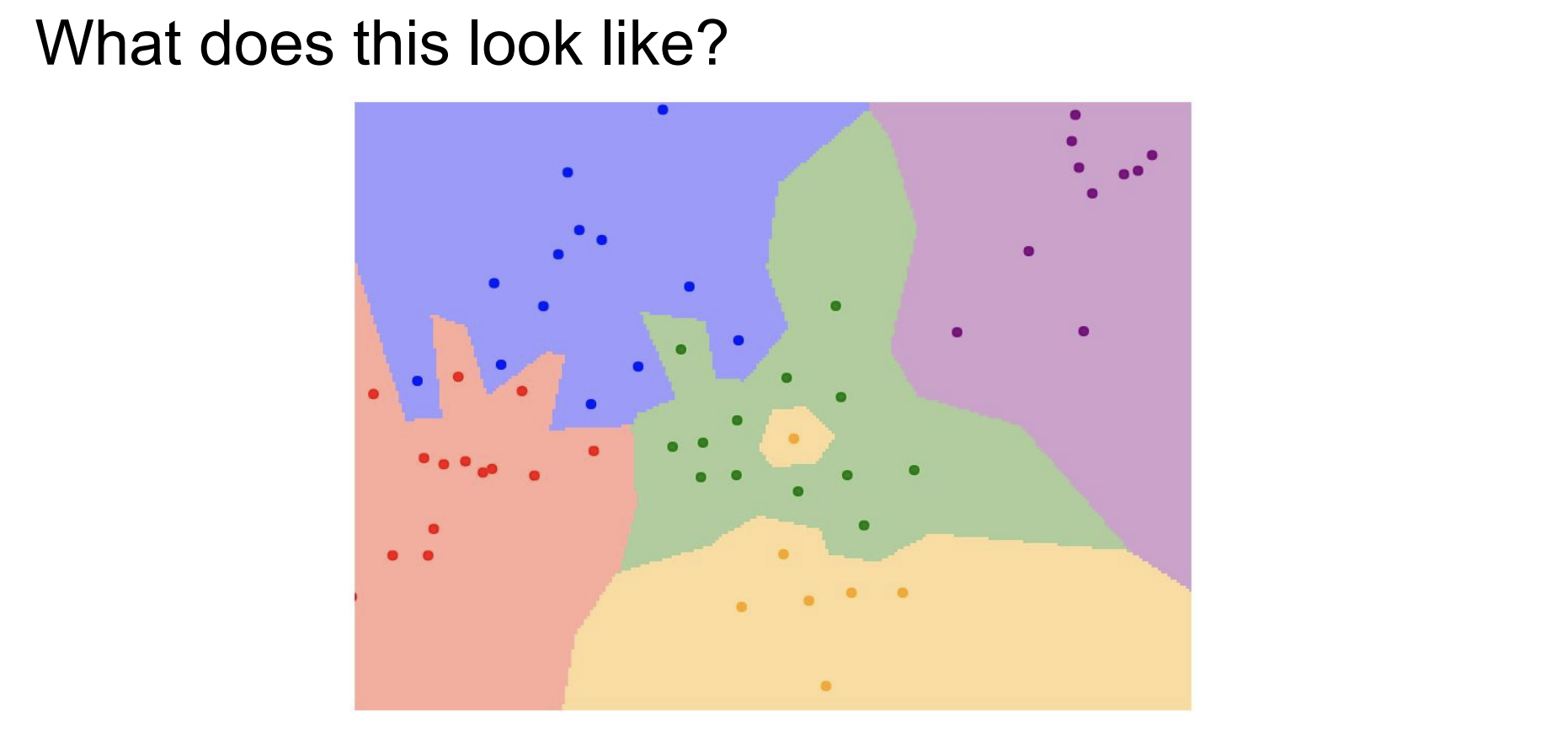
결과적으로도 좋지 않다. 단순 NN을 통해 분류하였기 때문에 경계선이 완만하지 않고, 특히 초록 영역에 노란 sample이 할당된다는 것은 classifier의 일반화 측면에서 매우 좋지 않다는 것을 알 수 있다.
따라서 등장한 접근법이 K-Nearest Neighbors(KNN)이다.

NN과 똑같이 distance를 구하여 하나의 스칼라 값으로 표현된 것을 바로 label로 분류하는 것이 아니라
가장 작은 값을 올림차순 했을 때 그중 상위 K개에서 voting 하는 방식으로 분류가 된다.
가령 K=3이고 올림차순 한 값이 10, 13, 15이면서 강아지, 고양이, 강아지라면 해당 test image는 강아지가 되는 것이다.
또한 distance를 측정할 때 L1 뿐만 아니라 L2 distance까지 고려한다고 한다.
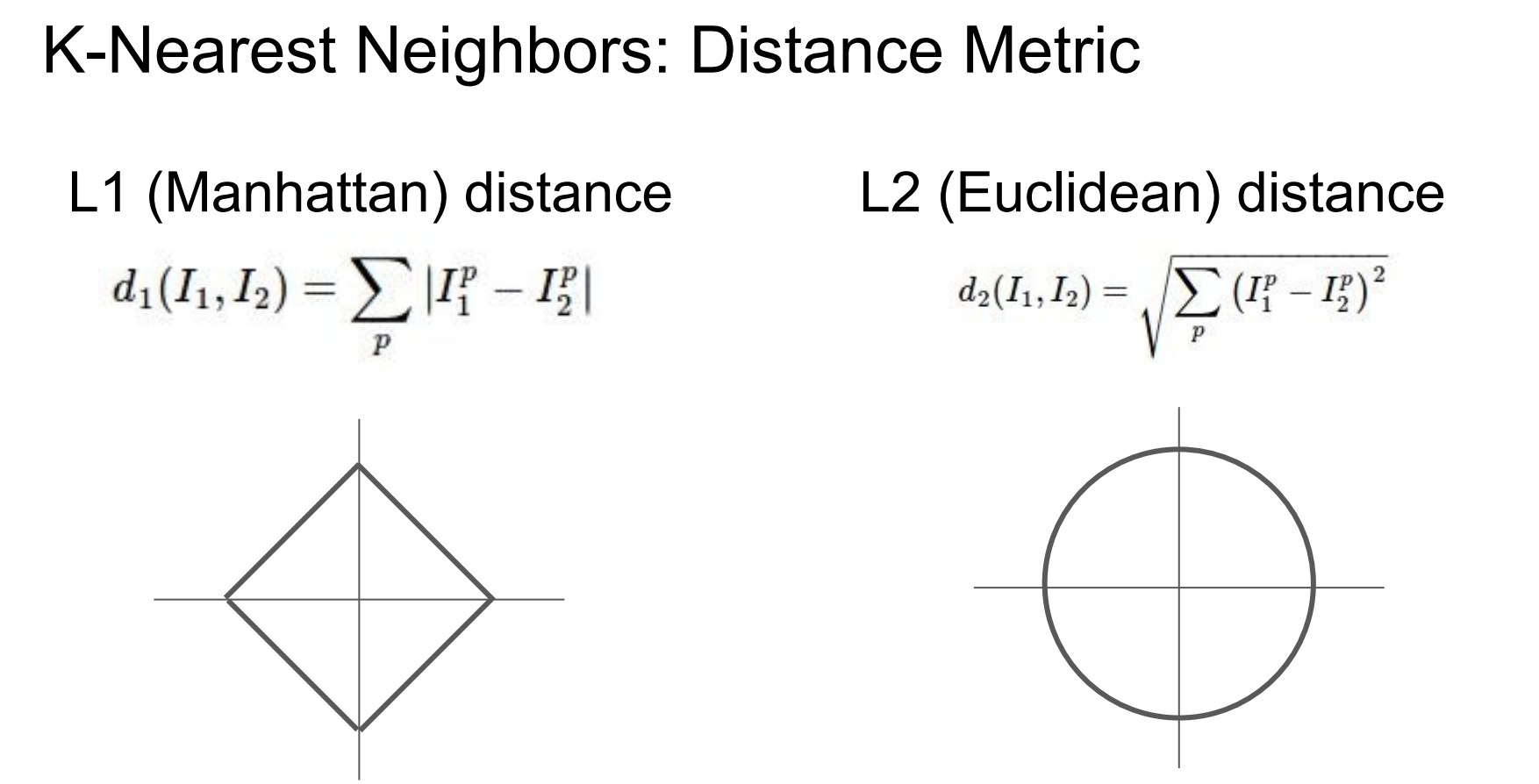
이렇게 되면 우리가 정할 수 있는 hyperparameter가 2개가 생기게 된다.
하나는 K를 얼마로 할지, 다른 하나는 L1/L2중 어떤 것을 사용할지이다.
이는 preblem-dependent 하므로 모두 적용해 보고 나은 것을 선택하는 것이 필요하다.
data-driven approach에서 hyperparameter를 setting 하는 데 train/validation/test dataset을 나눠 validation set에 적용해 보고
평가는 test에서만 이뤄지게 하는 것을 권장한다.
특히 small dataset에서는 이를 나누게 되면 sample이 매우 적어지므로 cross-validation 기법을 사용하는 것이 효과적이다.


이렇게 최적의 k와 distance metric를 구하더라도 KNN은 사용되지 않는다.
첫 번째 이유는 NN과 마찬가지로 test time이 너무 길고, 이미지 전역에 대한 각 픽셀의 distance의 합은 not informative 하기 때문이다.

not informative 하다는 것은 위의 그림 2를 보면 이해하기 쉽다.
원본 이미지에서부터 모두 같은 distance를 가지는 이미지들이다.
boxed / shifted / tinted 된 경우 모두에서 같은 distance를 가지고 있기 때문에 처음에 언급한 semantic gap의 문제를 해결하지는 못한다.
두 번째 이유는 Curse of dimensionality의 문제가 있기 때문이다.
이미지와 같은 고차원의 데이터(해상도만큼의 픽셀이 3차원으로 구성된 데이터)는 저 차원의 데이터에 비해 표현되는 능력을 제곱만큼 비례하게 된다. 아래의 그림 3을 보고 이해해 보자.

1차원에서 4개의 point로 표현되는 정도가 2차원에서는 4의 제곱만큼 필요하며, 3차원에서는 4의 세제곱만큼 필요하다.
이는 이미지 데이터를 KNN에 적용하는 것은 비효율적이라는 의미이다.
이에 linear function으로 classify 하는 방법론이 등장했다.
이때 등장하는 것이 neural network이다.
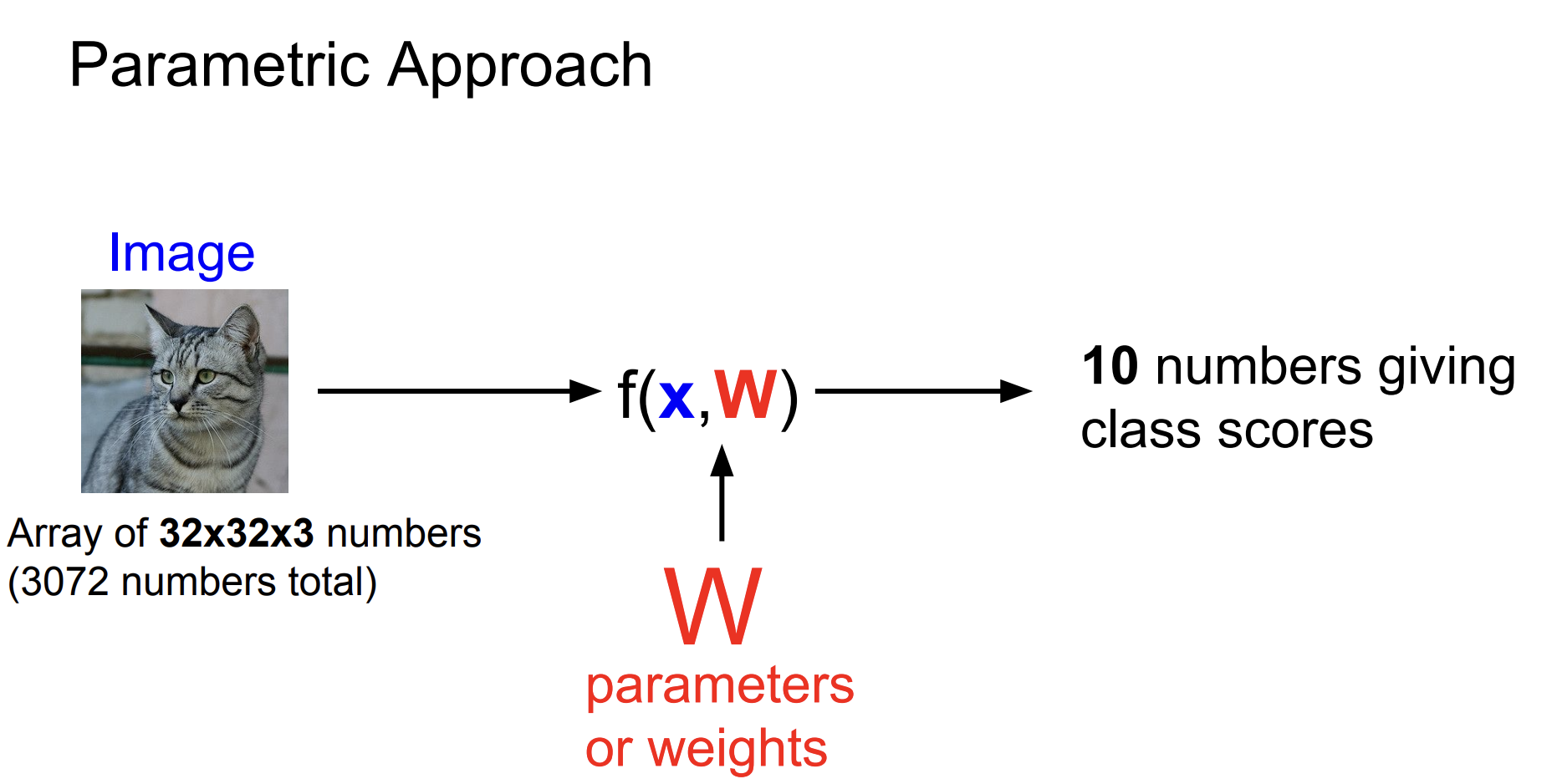
10개의 class를 구분하는 linear classifier의 parameter를 구해보자는 아이디어이다.
이 예제에서는 10개의 W가 각 class의 점수를 부여하고 이를 분류에 활용하는 것이다.
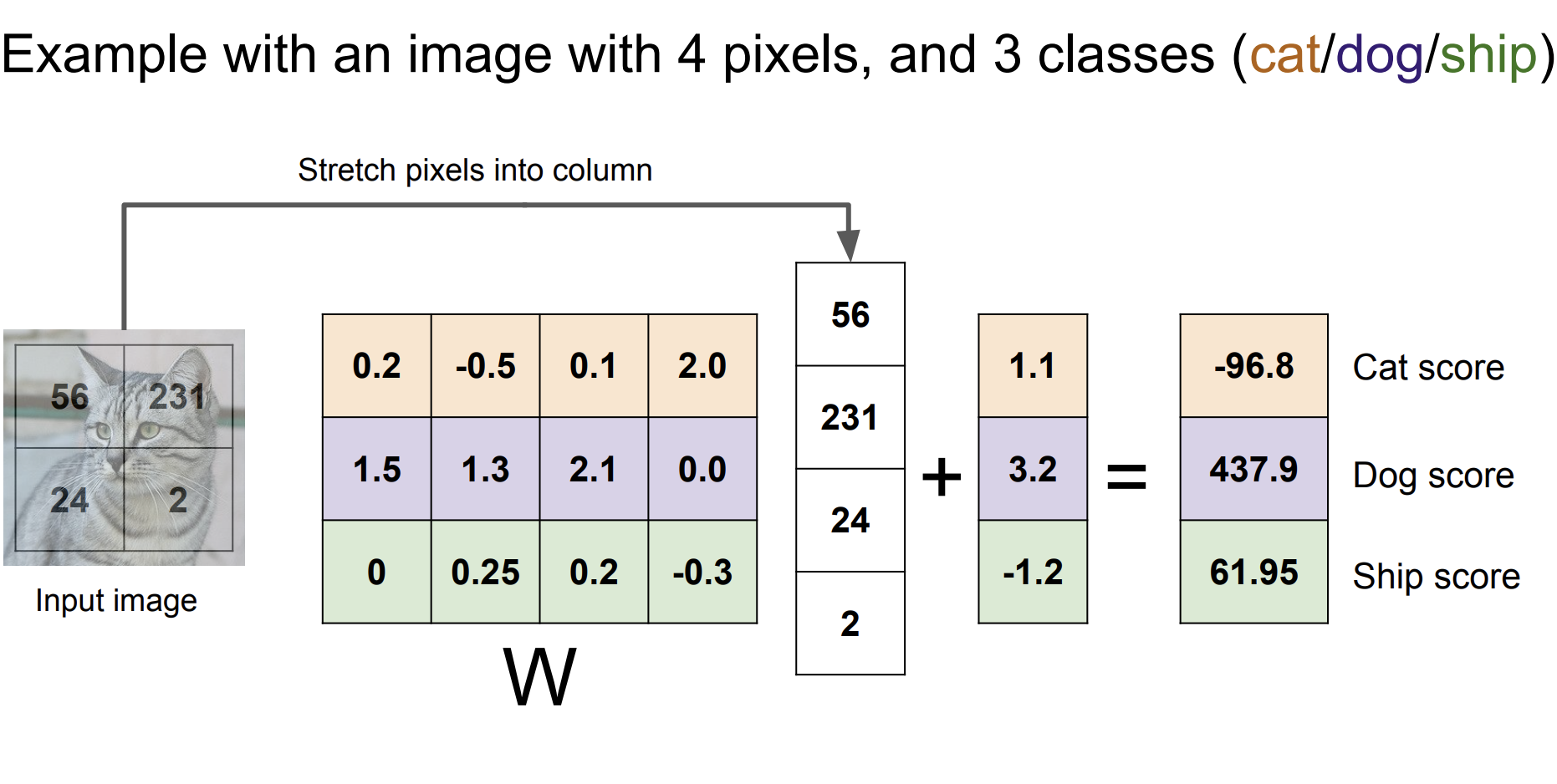
그럼에도 Linear classifier 역시 문제가 많다.
공간의 정보를 활용하기보다는 픽셀 값 자체를 활용하여 분류하는 데 사용했기 때문이다.
실제로 trained weights의 example을 보면 형체는 알아볼 수 없는 채로 표현이 되고 있다는 것을 알 수 있다.

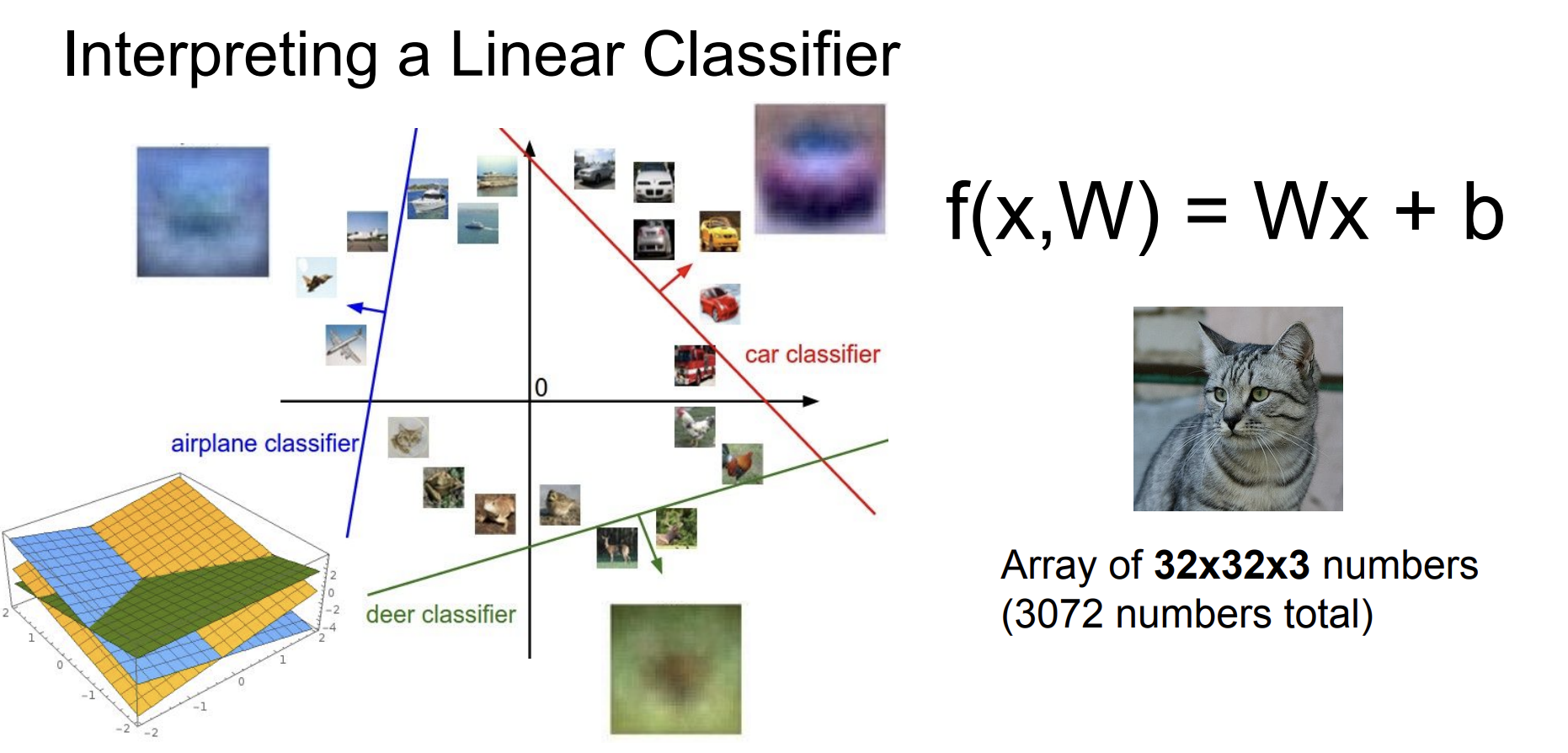
더욱이 어떠한 형태의 데이터는 linear classifier가 잘 분류하지 못하게 된다.
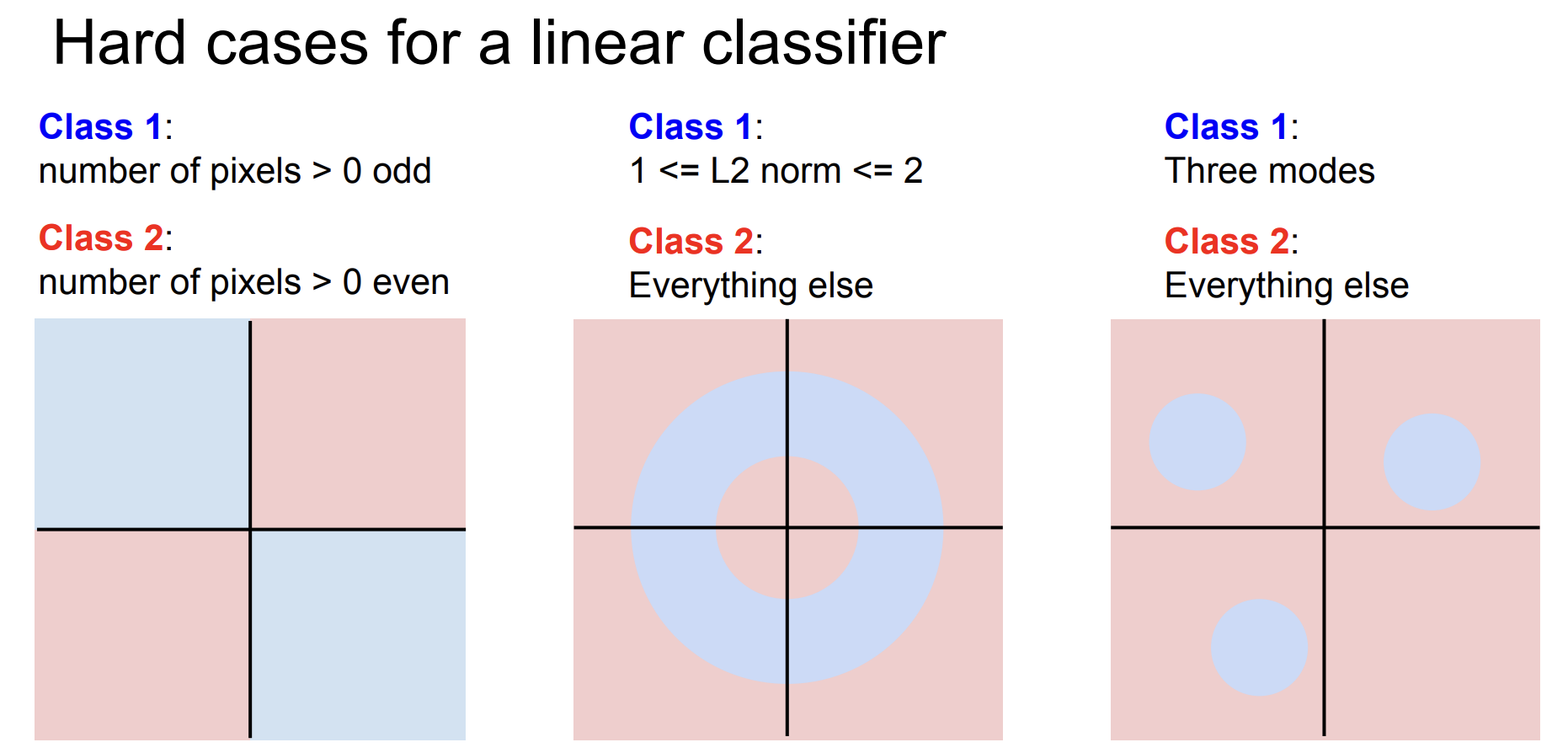
따라서 Linear classifier도 이미지 데이터를 다루는 데 근본적인 문제가 있다.
이를 해결한 접근법이 CNN이다.
이는 추후 다른 chapter에서 다루므로 그 때 설명하도록 하겠다.
reference
[1] lecture slide, http:// https://cs231n.stanford.edu/2017/syllabus.html
'인공지능 > cs231n' 카테고리의 다른 글
| [cs231n] 5강. Convolutional Neural Networks (0) | 2024.06.19 |
|---|---|
| [cs231n] 4강. Backpropagation and Neural Networks (0) | 2024.06.05 |
| [cs231n] 3강. Loss functions and Optimization (2) | 2024.05.28 |