이번 5강에서는 Vision Task를 효율적으로 해결하는 네트워크 구조인 Convolutional neural network의 역사와 작동 원리에 대해 알아본다.
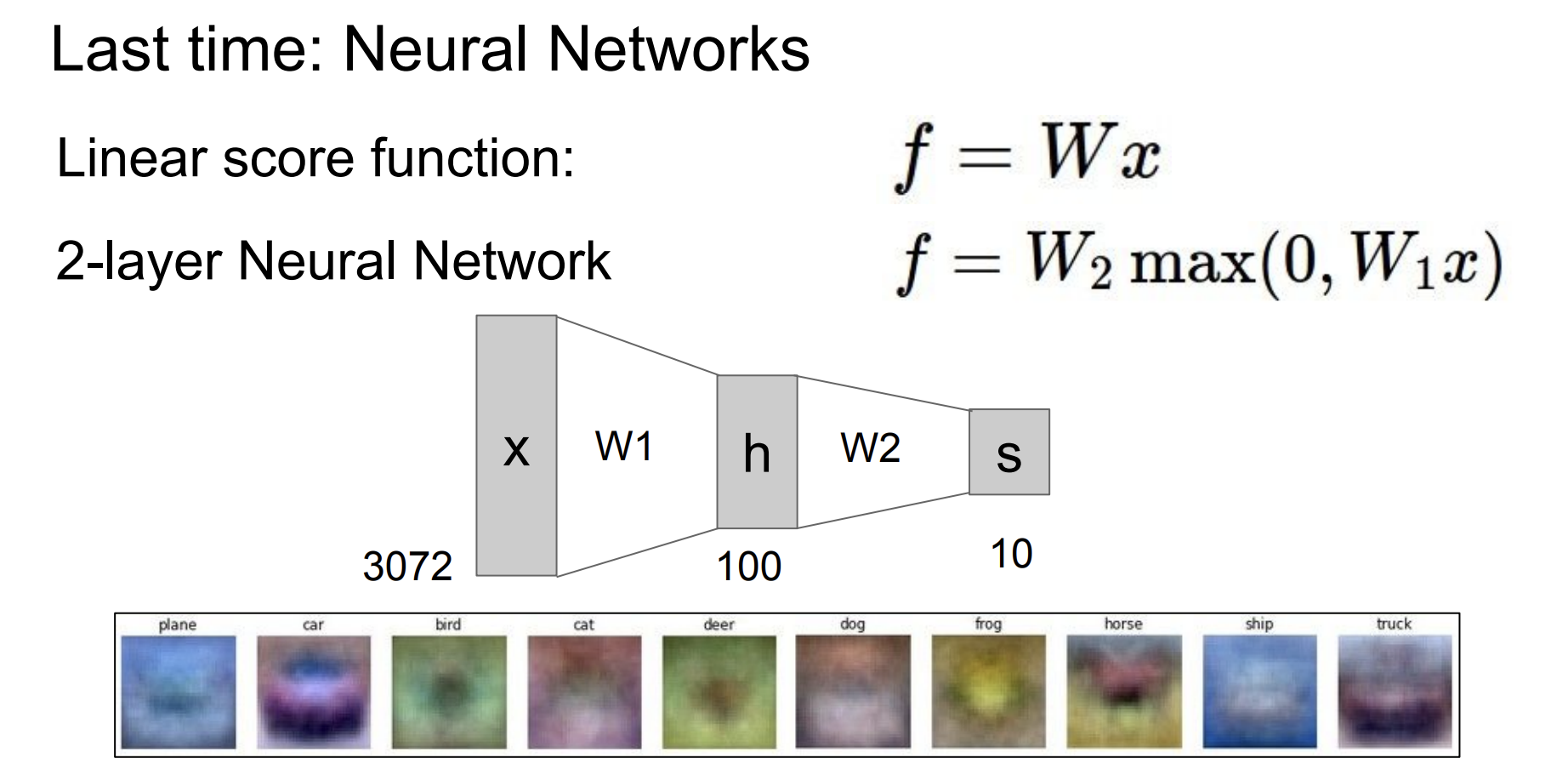
지난 시간에 배운 내용은 위 그림과 같다.
2개의 퍼셉트론 층을 쌓았다.
단순히 선형 변환식을 겹쳐서 쌓아 최종 스코어를 얻었다.
이는 명확하게 한계가 있다.
각 이미지의 지역적 정보를 활용하지 못할뿐더러 각 입력이 모든 출력에 개입한다는 점이 그렇다.
이러한 한계점을 CNN이 해결해준다.


CNN의 등장 배경의 역사를 거슬러 올라가면 아주 오래전으로 거슬러 올라간다.(1957년)
그러한 배경은 차치하고 CNN 등장에 가장 직접적인 역할을 한 것은 LeCun의 모델이다.
위의 왼쪽 그림이 LeCun의 모델의 구조인데 사실 CNN과 거의 똑같다. 다만 스케일에서 차이가 있다.
이 모델은 gradient기반의 backpropagation이 가능하면서 이미지의 지역적 특징을 잘 잡아낸다.
이 모델은 document recognition에 활용되었다고 한다.
이러한 아이디어를 기반으로 다양한 CNN 기반 모델이 탄생하였고(ex. Alexnet), 많은 Vision task에서 큰 두각을 나타냈다.



이미지 분류, 이미지 검색, 객체 탐지 등등 매우 다양한 도메인과 task에서 CNN이 사용된다.
이러한 CNN 모델을 활용하려면 개념과 작동 원리를 알아야 한다.
5강에서 이를 설명해 준다.

우선 우리는 지금까지 선형 결합을 위한 Weights에 대해 공부했다.
위의 그림을 보면 Fully conneted 하게 만들기 위해 input으로 32*32*3 픽셀 크기의 이미지를 3072차원의 벡터로 표현했다.
이에 대한 10 * 3072차원 크기의 weights를 부여하여 dot product(내적) 연산을 하면 10개의 결괏값이 나온다.
즉, Fully conneted layer에서 3072차원의 입력에 대한 각 weight의 dot products의 결과는 하나의 number가 되는 것이다.

반면에 Convolution layer는 하나의 number를 계산하는 방식이 조금 다르다.
입력 이미지의 크기와 차원을 그대로 둔 상태로 공간적으로 내적 하여 하나의 number를 도출하는 방식을 사용한다.
위의 예시를 보면 32 * 32 * 3 크기의 이미지 입력이 차원 그대로 들어오면 5 * 5 * 3 크기의 filter를 구성하는 W와 곱해지고 bias를 더하여 하나의 number를 만드는 것을 알 수 있다. (편의를 위해 이를 Conv연산이라고 하겠다.)
이런 식의 계산을 슬라이딩하면서 모든 이미지에 대해 적용하면 전체 이미지에 대한 activation 1개를 구할 수 있게 된다.
여기서 activation map은 슬라이딩 한번 당 filter가 계산된 값(score 값의 역할)들을 모아놓은 map이라고 생각하면 된다.


전체 이미지에 또 다른 필터를 (다른 값으로 이뤄진 W의 filter) Conv연산을 하게 되면 또 다른 activation map이 나오게 된다.
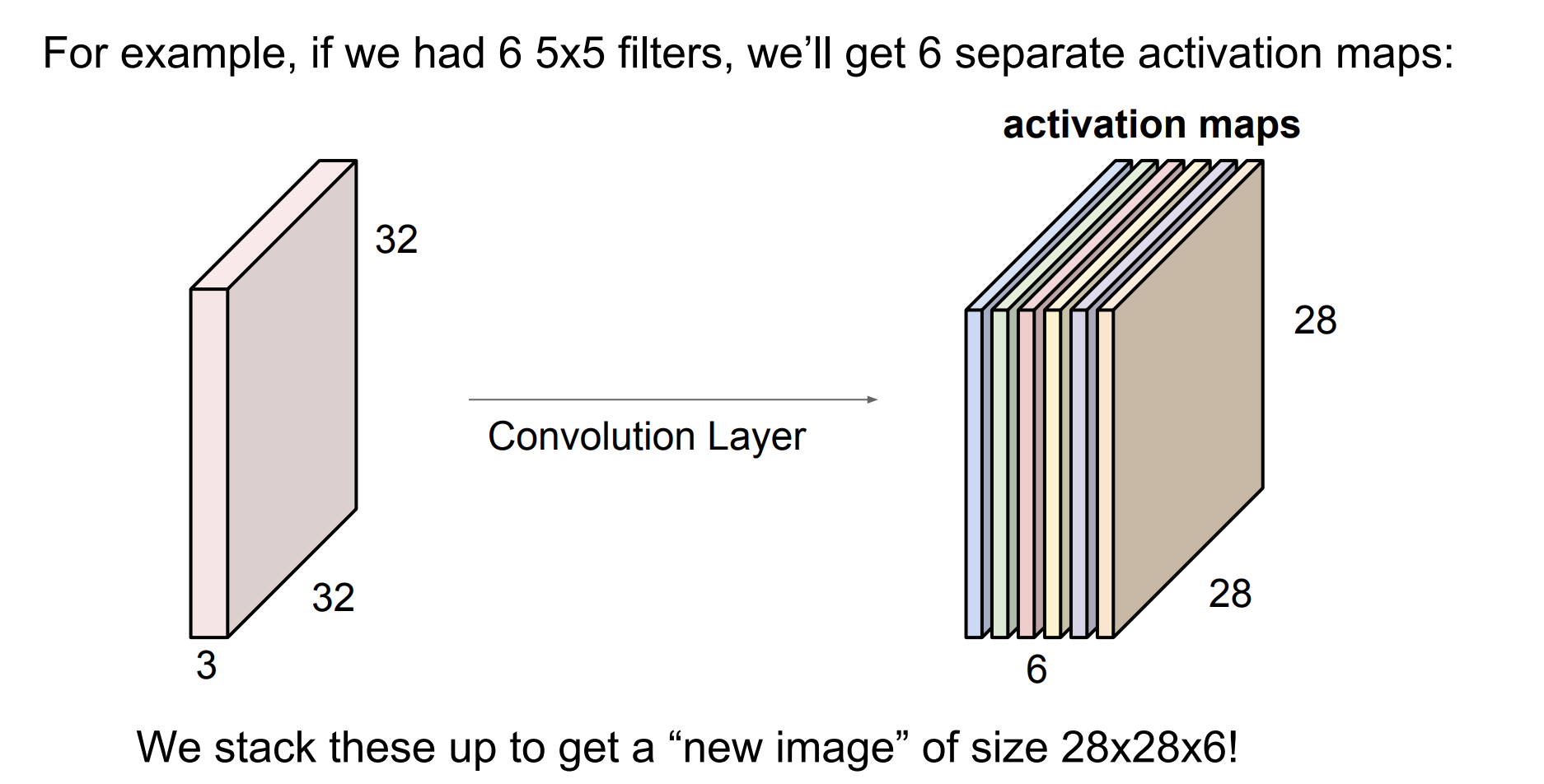
위의 예시를 보면 이와 같은 방법으로 6개의 filter를 사용하여
총 6개의 28 * 28 * 6 크기의 activation map을 만들어 낸 것을 볼 수 있다.

그렇게 나온 activation map을 입력으로 (하나의 이미지로 간주하듯이) 계속해서 Conv layer를 쌓은 것이 CNN이다.
(입력 -> conv 연산 -> activation function -> 출력) -> 반복
각 conv layer의 출력이 어떠한 특징들을 뽑아내는지 시각적으로 알 수 있다.

VGG라는 Conv 모델에서의 layer 깊이에 따라 activation map을 시각화한 것이다.
low level은 입력에서 가까운 conv layer의 출력인데, 세로선, 가로선과 같은 low level의 feature가 추출되는 것을 볼 수 있다.
Conv layer를 지날수록 나오는 특징은 mid level과 high level에서 볼 수 있듯이 다소 추상적으로 변한다.

image classification task에서 CNN은 전통적으로 위 그림처럼 쌓는다.
중간에 나오는 pooling layer는 무슨 역할을 할까?
결과적으로는 activation map을 대표되는 값으로 downsampling 하는 역할을 한다.
즉 map의 크기를 줄이는 것이다.
pooling 말고도 Conv 연산에서도 downsampling이 이뤄진다.
7 * 7 input 이미지에 대해 3 * 3 filter를 conv 연산 적용하여 3 * 3의 activation map이 나오게 하려면
2칸씩 띄어 슬라이딩해야 할 것이다. 이 간격을 stride라고 한다.


그렇다면 같은 조건에서 stride를 3으로 하면 어떻게 될까?
이는 맞지 않는다.


output size는 위 오른쪽 그림과 같은 식으로 도출된다.
한 칸 단위로 2.33의 칸을 표현할 수 없기 때문이다.
Conv layer를 구성할 때 filter size, stride는 하이퍼파라미터가 된다.
이렇게 계속해서 downsampling 했을 때의 단점이 존재한다.
원본 이미지에 대하여 가장자리에 있을수록 conv 연산의 결과에 기여하는 횟수가 적어진다는 것이다.
(모서리쪽 정보를 활용하기 힘들다.)
또한 계속해서 줄어드는 size로 층을 깊게 할 수 없다는 점이다.
이러한 한계점을 극복하고자 등장한 개념이 padding이다.

padding기법은 가장자리 위에 0과 같은 동일한 숫자로 감싸주는 것을 의미한다.
위의 예시처럼 7 * 7 input에 1 pixel만큼 padding을 해주면 9 * 9 크기가 될 것이다.
이를 stride 1로 3 * 3 filter를 적용하면 output은 7 * 7로 input과 같은 size가 된다.
일반적으로 stride 1을 기준으로 filter 크기가 3이면 1만큼, 5이면 2만큼, 7이면 3만큼 zero-padding 해준다고 한다.
뉴런의 관점에서 보면 각 activation map은 뉴런 output의 모임이라는 것을 또다시 강조한다.
이는 input에 대하여 작은 지역만큼(filter size만큼) 연결되어 있다는 의미이고(=filter 크기만큼 연산이 되어 하나의 값이 된다)
같은 filter를 사용하기 때문에 parameter를 share 한다는 것이다.


또한 오른쪽의 그림처럼 각 다른 filter가 적용되면 같은 위치의 이미지를 다른 filter로 계산하는 것은
보다 풍부하고 유의미한 특징을 추출하는 것임을 알 수 있다.


앞서 언급했듯이 downsample의 기능을 수행하는 또 다른 CNN의 구조는 pooling layer이다.
크게 max pooling과 average pooling이 있는데 여기서는 max pooling의 예시를 든다.
pooling에서도 이를 적용할 filter size가 필요한데 그 size안에서 가장 큰 값을 대푯값으로 뽑는 것이다.
따라서 이 layer에서는 학습 파라미터는 없다.
Reference
[1] CNN 연산, https://sanmldl.tistory.com/28
[2] 강의 노트, https://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture5.pdf
'인공지능 > cs231n' 카테고리의 다른 글
| [cs231n] 4강. Backpropagation and Neural Networks (0) | 2024.06.05 |
|---|---|
| [cs231n] 3강. Loss functions and Optimization (2) | 2024.05.28 |
| [cs231n] 2장. image classification pipeline (0) | 2024.05.24 |


