이번 4강에서는 backpropagation의 작동 원리와 Neural network의 아키텍처에 대해 간략히 알아본다.


지금까지 배운 것은 다음과 같다.
이미지에 대한 score를 구하고 이 값을 Loss function에 적용했다.
그 후에 Data loss를 구하여 w(파라미터)에 대한 data loss의 기울기를 구했다.
이때 gradient descent 방식이 사용되어 최적의 loss를 갖도록 파라미터를 업데이트 했다는 것이다.

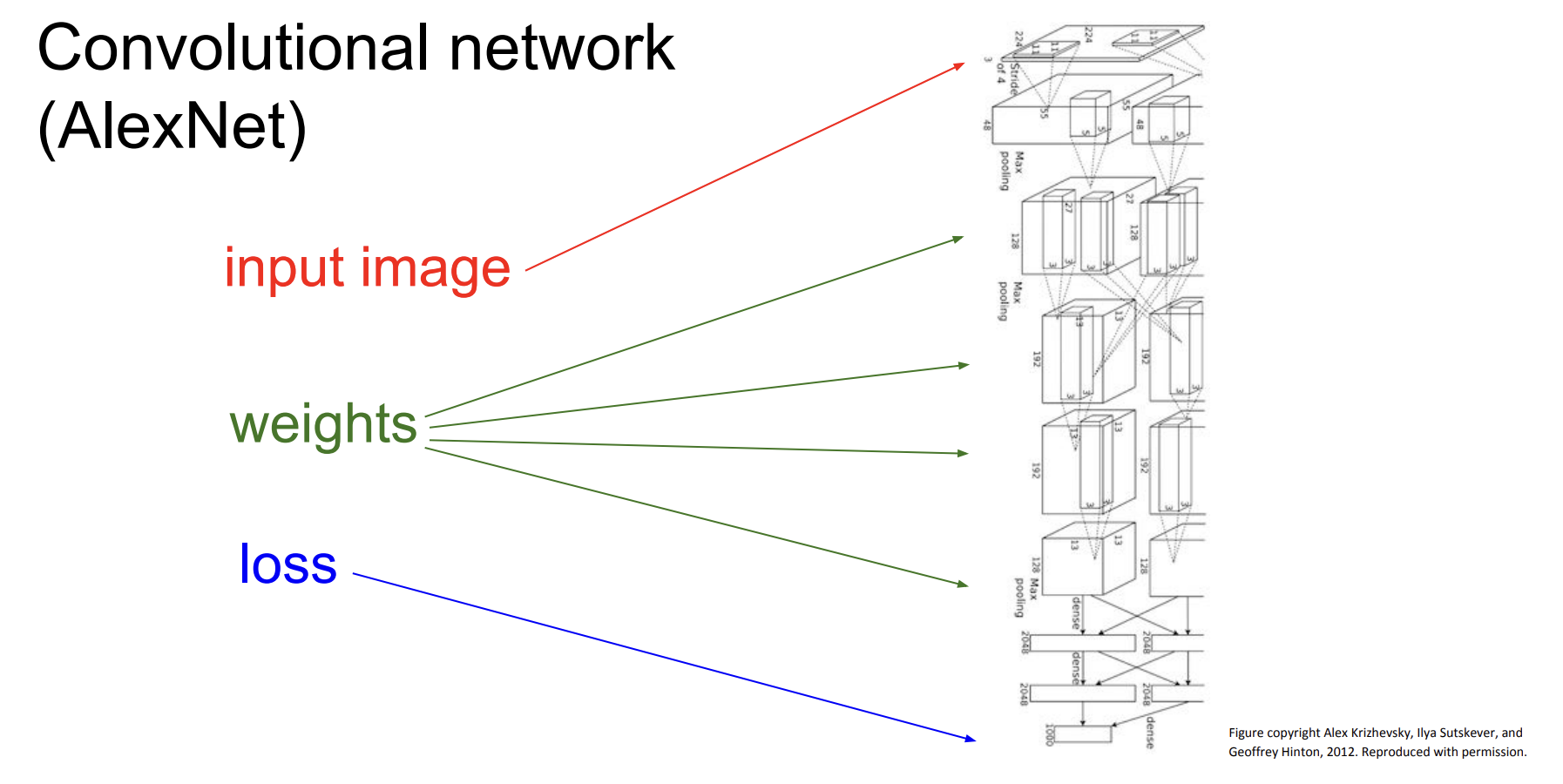
위 그림에서 알 수 있듯이 입력 이미지로부터 loss까지 도달하기에 수 많은 weights(model parameter)가 있다.
기울기를 구하는 건 알겠는데, layer를 거치면서 생기는 이 많은 weights의 기울기는 어떻게 한번에 구할 수 있을까?
이 물음에 답변을 해주는 것이 backpropagation이다.
여기 간단한 backpropagation의 예시가 있다.

x,y,z를 입력으로 하는 함수 f(x,y,z)가 있다고 하자.
x,y,z에 대한 값을 대입하면 (x+y)z 식에 의해 값이 도출된다.
(여기서 x,y,z는 -2, 5, -4이다.)
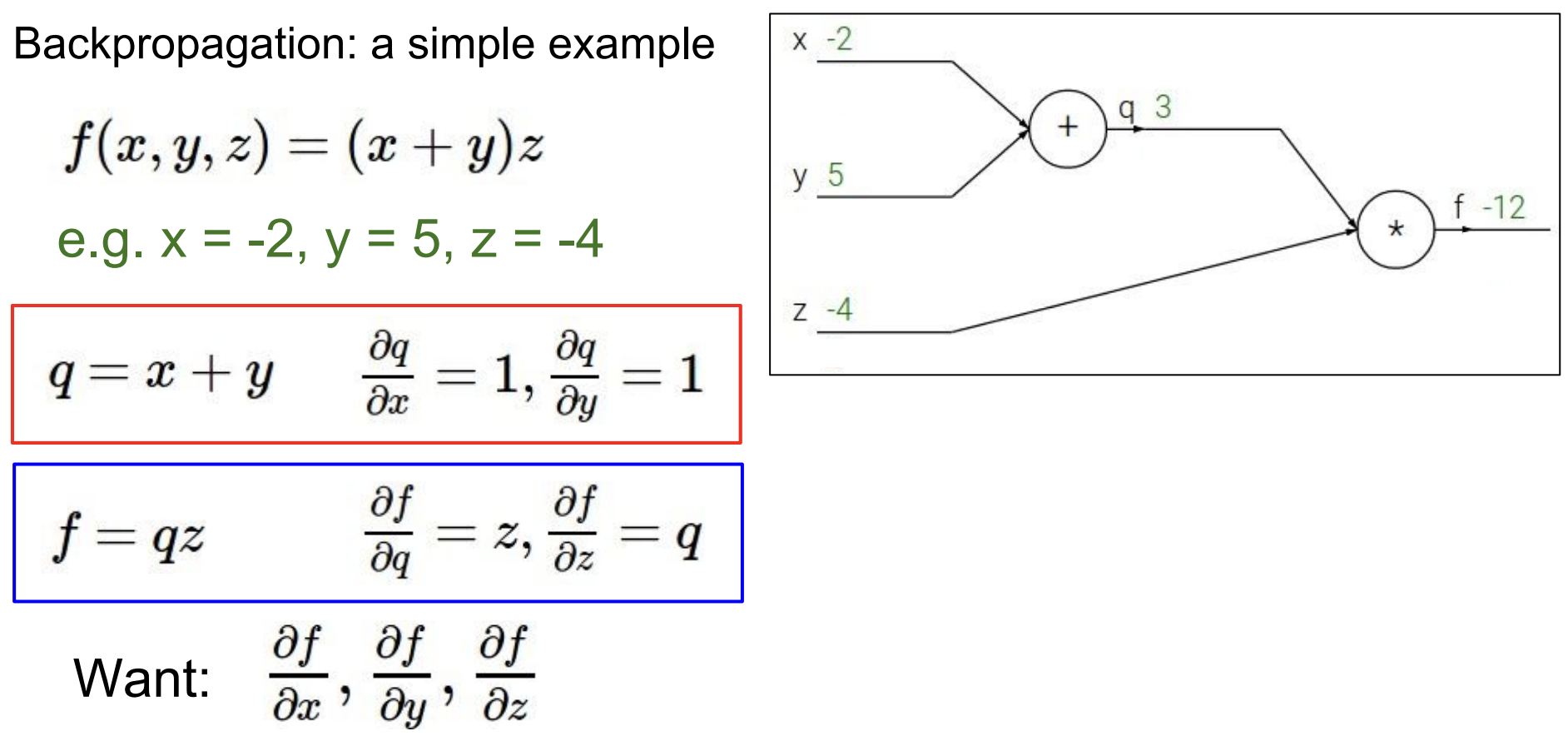
덧셈에 대한 미분은 1이 되고, 곱셈에 대한 미분은 서로의 계수가 된다.
이것까지 알면 이 예제에서의 backpropagation은 거의 끝났다.
이제 위의 f출력에서부터 거슬러 내려오면 된다. 반대 방향으로 흘러 들어오기 때문에 backpropagation이라고 한다.
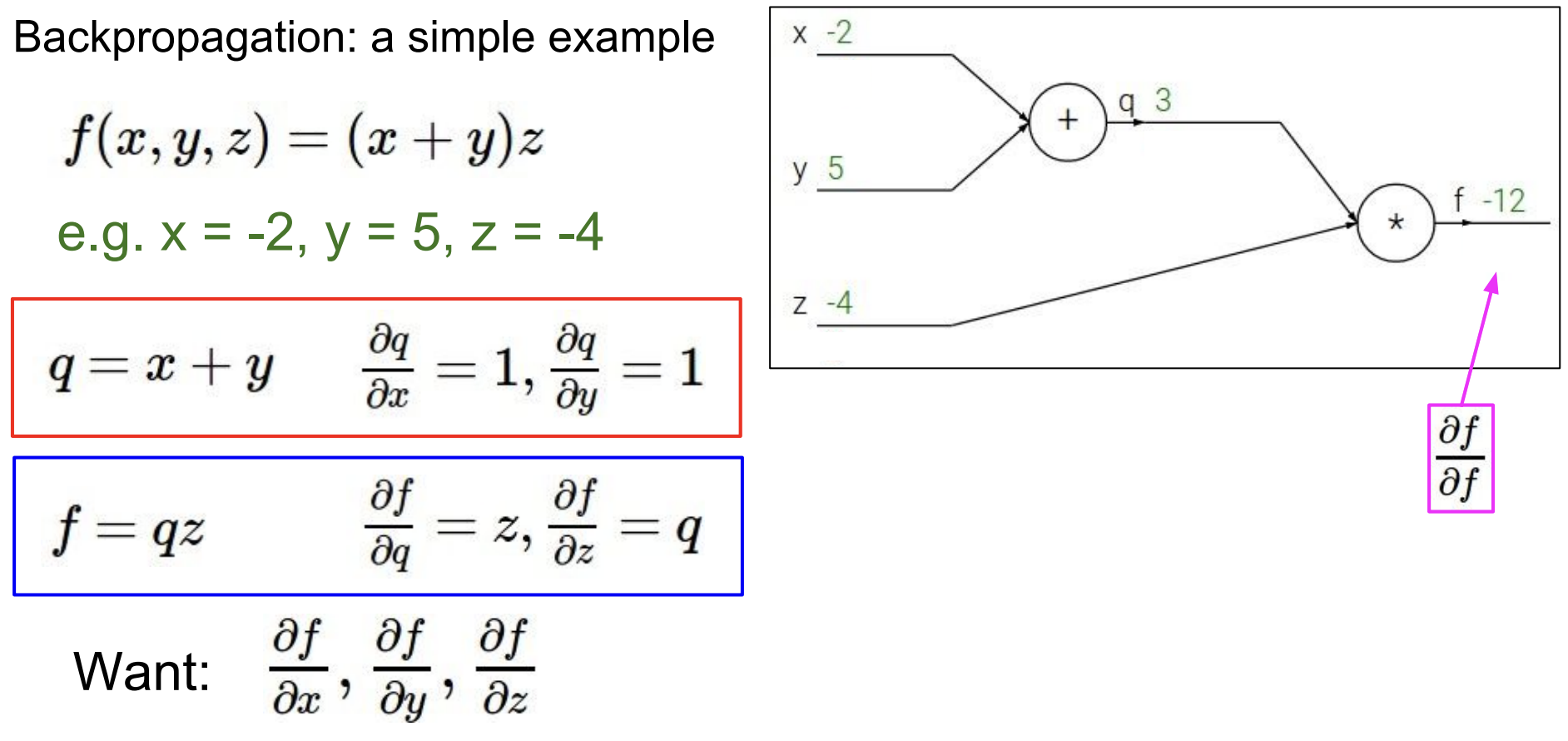
\(\frac{\partial f}{\partial f}\) 는 자기자신에 대한 미분이므로 1이된다.
이 기울기('1')은 위의 q와 아래의 z로 흘러들어간다.
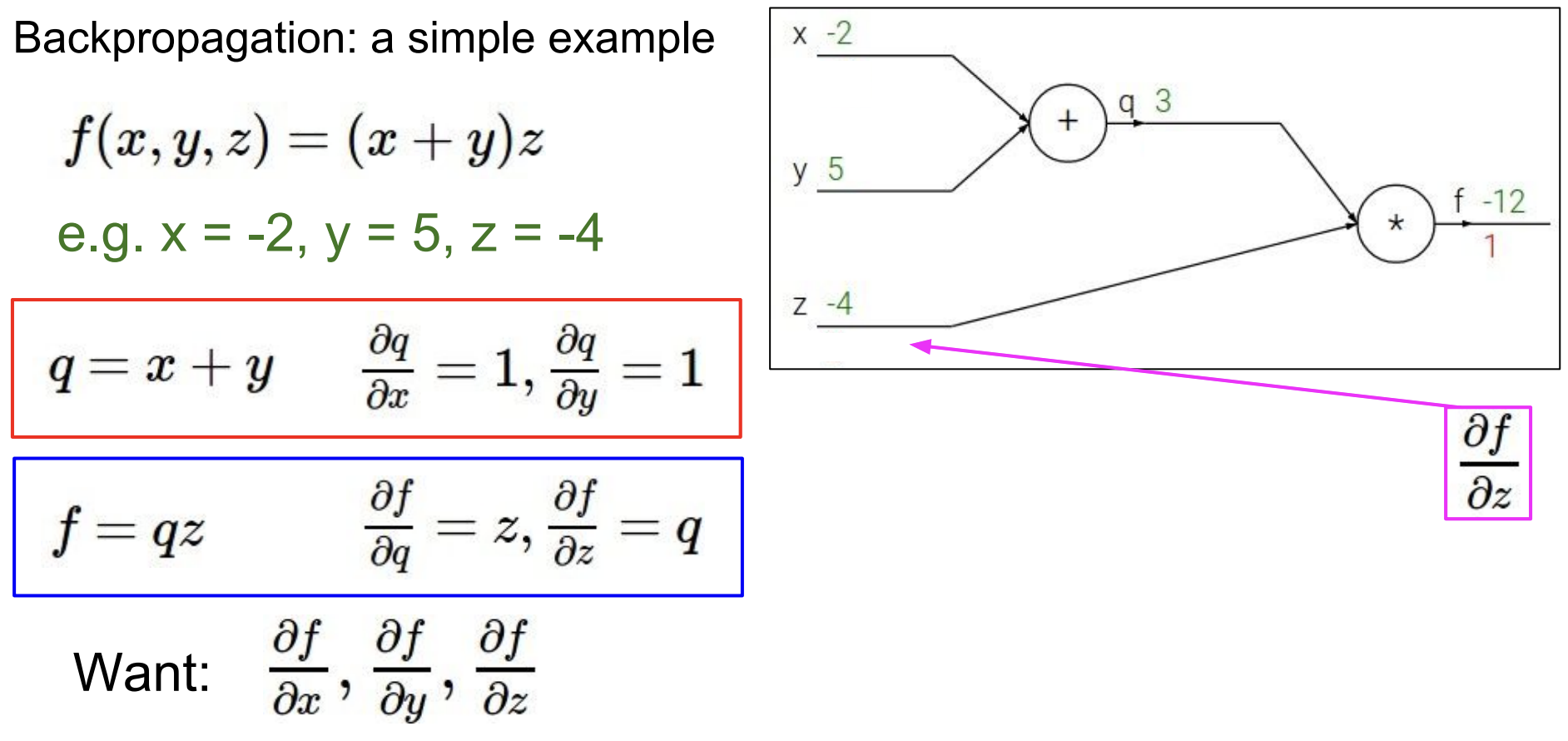
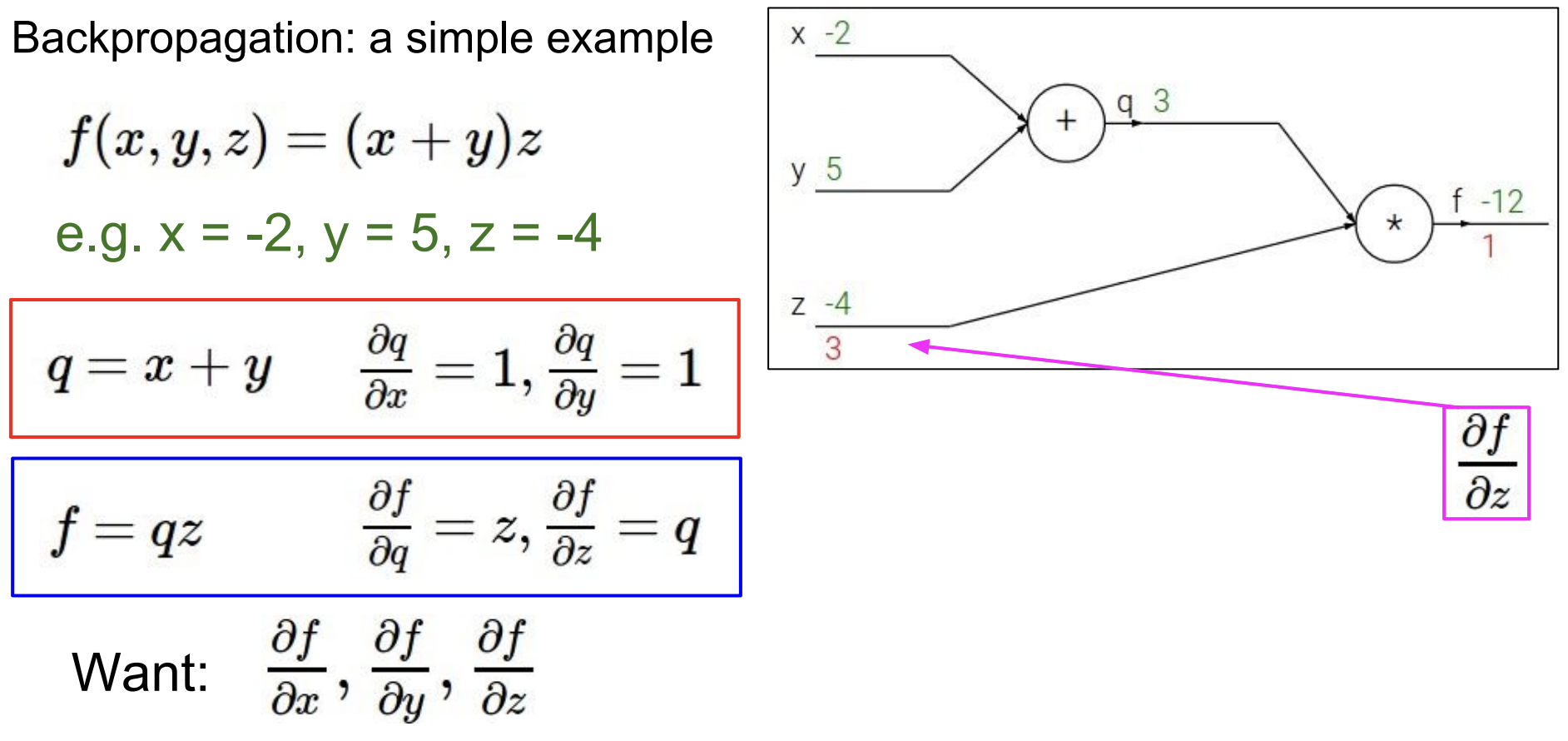
우선 z로 들어가면 곱의 미분이 적용되므로 계수인 q가 기울기가 된다.
이때 chain rule이 적용되어 흘러들어온 1과 z에서의 기울기 3을 곱한 3이 최종 기울기가 된다.
chaine rule이란?
직역하면 연쇄법칙으로, 합성함수의 미분을 의미한다.
x에 대한 함수가 있고 t에 대한 함수가 x라고 한다면 우리는 합성함수로 이를 표현할 수 있다.
y=f(t), t=g(x) -> y=(f(g(x)))
각 함수에 대한 미분계수를 구하면 \(\frac{\partial t}{\partial x}\)와 \(\frac{\partial y}{\partial t}\)를 구할 수 있다.
따라서 다음과 같은 식이 성립한다.
\(\frac{\partial y}{\partial x}\) = \(\frac{\partial y}{\partial t}\) * \(\frac{\partial t}{\partial x}\)
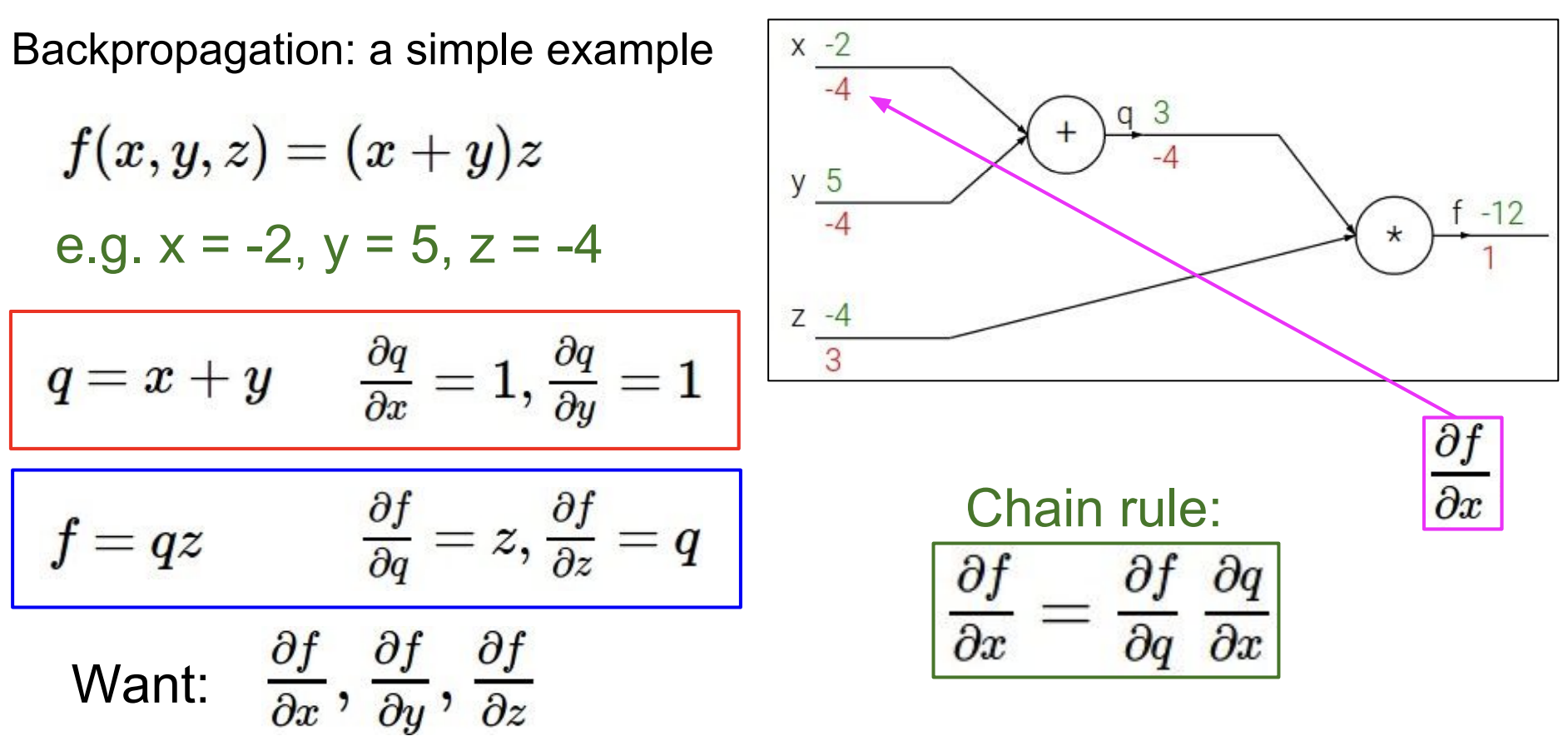
위로 흘러들러가는 경우도 똑같다.
chain rule에 의해 위에서 흘러들어온 기울기인 1과 계수인 z의 값-4를 곱하여 해당 기울기를 구한다.
그 후 x,y 방향으로 흘러들어갈때는 덧셈에 대한 미분이므로 -4가 그대로 흘러들어간다.
이렇게 되면 각 x,y,z에 대한 f의 기울기를 구할 수 있게 되는 것이다.

위 그림은 backpropagation의 각 연산에 대한 과정을 보여주고 있다.
각 입력으로부터 출력을 계산하고 그 출력으로부터 기울기를 구한다.
위에서 흘러들어온 gradient(global gradient라고도 함)와 해당 연산에 대한 기울기를 구하여 곱한다.
이것을 가능하게 하는 것은 chain rule 덕분이다.
그렇게 계산된 기울기는 그 다음 기울기를 구하기 위한 global gradient가 되어 다시 사용되는 것이다.
(이후의 4강의 backpropagation의 과정은 이 큰 틀에서만 이뤄지기 때문에 직접 보면서 해결해보는 것을 추천한다.
다만 연산에 따른 미분이 달라진다는 것과 vectorized example에서 행렬에 대한 미분은 형태까지 고려해야한 다는 것만 주의하면 될 것 같다.)
다음 내용은 Neural network에 관한 것이다.

이전에 우리는 linear regressor를 통해 score function을 구했다.
이에 neural network는 이 linear regressor를 2층 3층 쌓아 score function을 구해보자는 아이디어이다.

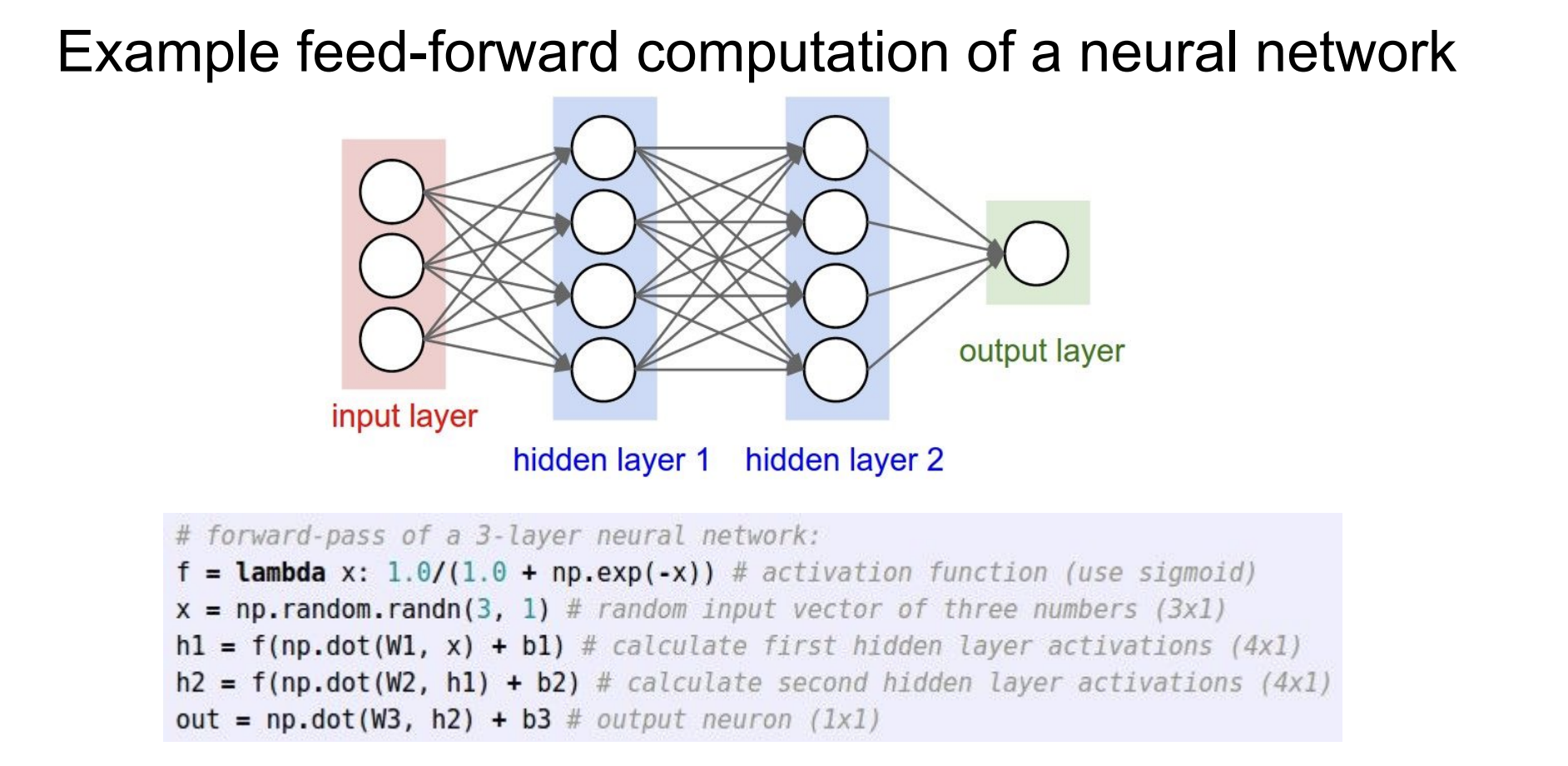
Neural network의 아키텍처는 각 노드들이 fully-connected 되어있다. 즉 모든 입력이 모든 출력에 영향을 끼치는 것이다.
몇 개의 layer를 쌓았느냐에 따라 2-layer, 3-layer... network라고 부른다.
또한 우리가 앞에서 score를 구할 때 하나의 linear한 계산식을 사용했다.(w를 곱하고 b를 더한다)
층을 더한다는 것은 이것을 합성함수처럼 계속 적용하겠다는 의미이다.
실제로 computation 예제를 보면 각 linear 연산을 반복해주는 것을 알 수 있다.
reference
[1] 4강 slide, https://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture4.pdf
'인공지능 > cs231n' 카테고리의 다른 글
| [cs231n] 5강. Convolutional Neural Networks (0) | 2024.06.19 |
|---|---|
| [cs231n] 3강. Loss functions and Optimization (2) | 2024.05.28 |
| [cs231n] 2장. image classification pipeline (0) | 2024.05.24 |


