3장은 지난 2장에서 살펴본 Linear classifier의 score가 얼마나 잘 산출된 것인지 알아보는 Loss func와
이 Loss func를 최소화시키는 parameter들을 얼마나 효율적으로 찾을 것인지 알아보는 optimization에 대한 내용이다.
앞서 우리는 linear classifier로 score를 산출할 수 있었다.
(이미지 픽셀값에 가중치 W행렬을 곱하고, bias를 더하여 score를 구했다.)
3개의 이미지에 대한 각 class의 score는 아래의 그림과 같다고 가정하자.

이 score의 합이 전체 데이터 셋에 대한 Loss에 기여하도록 해야 한다.
이 강의에서는 multiclass SVM loss를 사용하여 예시를 들어준다.
SVM loss에 따르면 고양이 이미지에 대한 Loss는 2.9가 된다.


이런 식으로 자동차, 개구리 이미지에 대한 score를 SVM loss에 적용한다면 다음과 같게 된다.
따라서 이 전체 데이터 셋에 대한 Loss는 각 이미지의 Loss의 평균이 된다.
= 5.27

직관적으로 생각했을 때도 "cat에 대한 값이 3.2로 두 번째로 높으니(실제론 가장 높아야 함) 적당한 Loss가 필요할 것이고, 반대로
frog에 대한 값이 -3.1로 터무니없는 값이 나왔으니(실제론 가장 높아야 함) 큰 Loss가 나와야 될 것이다"와 일맥상통하다.
(추가+) 아래의 6개의 Question에 대해 생각을 해보자.






그럼 Loss가 0인 parameter는 unique 한 것일까?
그렇지 않다.
SVM loss 식을 보면 Li = (잘못 분류한 score - 정답 레이블 score + 1(safety margin))이다.
정답을 맞히기만 하면, 즉 정답 score가 가장 높기만 하면 0보다 작은 값이 나올 것이므로 Li는 항상 0이 나오게 된다.
따라서 W에 2를 곱한 2W도 Loss가 0이 될 것이다.(3W, 4W .. 등등)
아래의 오른쪽 예시를 보면 이해하기 쉽다.


이는 적절한 W가 loss로 표현되는 것이 아니다.
2배, 3배 커진 W가 똑같이 loss를 0으로 표현한다는 것은 loss의 존재 의미에 위반하는 결과이다.
우리는 loss를 통해 w가 얼마나 최적화되어있는지를 알고 싶은 것인데,
loss가 0으로 같다는 것은 최적화가 되지 않았다는 뜻이기 때문이다.

뿐만 아니라 위의 그림처럼 data loss는 training data에 대해서 구해진 값이기 때문에
test data에 대해서 잘 작동하지 않을 수도 있다.
이는 train에만 잘 작동하는 W가 될 가능성이 매우 매우 크다는 뜻이다.
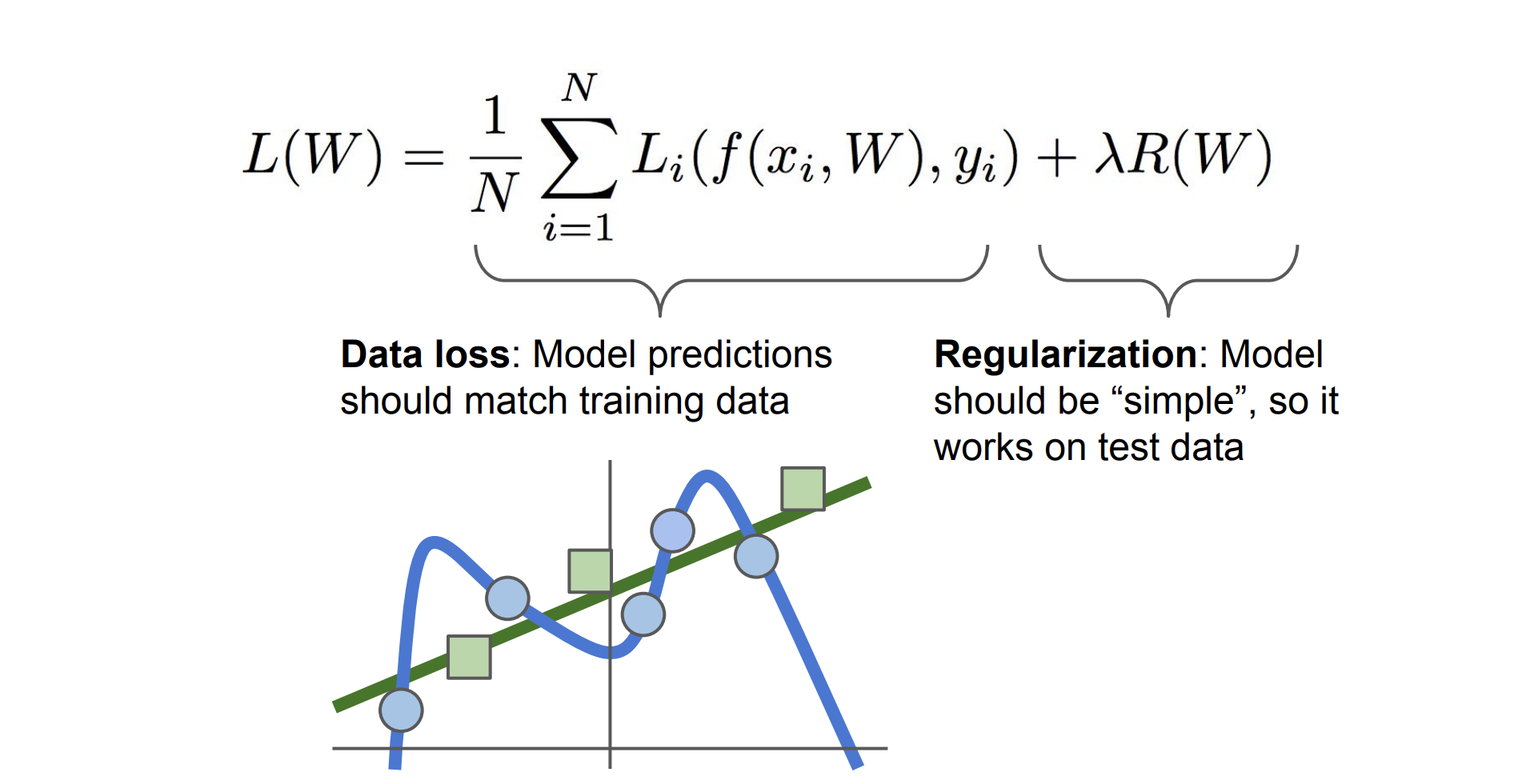

따라서 우리는 regularization이라는 기법을 사용하여 test data에도 어느 정도 잘 작동하도록 한다.
loss를 구할 때 어떠한 규제항을 더해줌으로써 전체 loss가 원래의 항뿐만 아니라 규제항에도 적용되어 loss가 무작정 줄어들거나 커지는 것을 방지하는 것이다.
(이전의 svm 예시처럼 W와 2W가 동시에 loss를 0으로 만든다고 하면 R(w)의 규제항이 이를 다르게 만들어준다고 생각하면 된다.)
일반적으로 쓰이는 regularization 기법은 오른쪽 그림과 같다.
보통 각 규제항에 쓰이는 식이 달라지는 것뿐이다.
더욱 자세한 내용은 추후의 강의에 있다고 한다.
분류 task에서 많이 사용되는 Softmax classifier에 대해 아는 것이 중요하다고 한다.
다중 분류에 사용되는데, 이미지 분류를 각 클래스에 대한 확률값으로 표현하고 이를 통해 분류하는 식이다.
그렇다면 score를 어떻게 확률값으로 표현할 수 있을까?
score를 정규화되지 않은 log probabilities로 만들고
이를 통해 나온 probability를 normalize 하여 각 class에 대한 확률값으로 표현하게 된다.
아래의 오른쪽 사진을 보면 계산 과정이 나타난다.


이 확률 값들의 log likelihood를 max 하는 것이 목표 중 하나가 된다.
쉽게 설명하면 모델이 고양이를 고양이라고 판단한 확률을 더 크게 만들어야 한다는 뜻이다.
여기서는 해석적으로 접근하면 모델이 고양이라고 판단할 확률이 0.13이고 car라고 판단할 확률이 0.87이라는 의미이다.

앞서 softmax classifier를 아는 것이 중요하다고 했는데, 여기서 요점이 나타난다.
이전의 svm의 hinge loss는 모두 같은 loss를 보이는 반면, softmax는 다 다른 값을 나타낸다.
왜 이게 중요한지는 이제는 이해할 수 있어야 한다.
Loss function에 따른 적절한 W가 필요하다는 건 알았는데, 그럼 어떻게 W가 적절한 방향으로 수렴하는 걸까.
이때 등장하는 개념이 Optimization이다.
Optimization을 처음 이해할 때 산꼭대기에 있는 등산가가 눈을 가리고 내려가는 것을 예시로 많이 든다.

눈을 가리고 산을 내려가는 것은 실제로 큰 위험이 있으니 불가능하다. 하지만 이러한 제약 조건을 빼고 가정한다면 눈을 감고 어떻게 산을 가장 빠르게 내려갈 수 있을까?
한 발자국씩 내딛을 때 가장 기울기가 가파르다고 판단되는 곳으로 내려간다면 빠르게 하산할 수 있을 것이다.
본 강의에서는 가중치 W를 수정해서 Loss가 최적의 점으로 수렴하는 것을 이에 비유한다.
그중 여러 가지 방법에 대해 설명해 준다.
1. Random search

random search 방법은 위의 예시 코드에서 알 수 있듯이 무작위로 W(parameter)를 조정하고 기존 Loss보다 작으면 해당 W를 채택하겠다는 전략이다.
이 전략은 강의에서 절대 하지 말아야 된다고 설명한다.
무작위성으로 인해 기대되는 성능이 나오지 않을 수 있기 때문이다.
2. Follow the slope

follow the slope 전략은 앞서 설명한 것처럼 발을 디뎌 내려가자는 아이디어이다.
그러기 위해서는 기울기를 구해야 하는데 이때 numerical descent 방식을 사용한다.
매우 작은 수를 더하여 그 방향으로 W를 바꿔나가고 이때의 기울기를 구하는 것을 의미한다.
이때 적절한 방향으로 W가 개선되었다면 음수의 기울기를 가질 것이다.

하지만 이에도 문제가 있다. 어떠한 방향으로 갈지 계산을 해봐야 알게 되는 것과 그 과정은 너무 계산 비용이 많이 든다는 점이다.
실제로 예시에서 W 벡터의 3번째 값을 아주 작은 방향으로 개선했더니 Loss가 증가했음을 알 수 있다.
또한 이를 마지막 값까지 직접 계산을 해줘야 기울기가 구해지므로 계산에 효율성이 좋지 않다는 것을 알 수 있다.
그래서 등장한 것이 3. Analytic gradient이다.


우리는 W에 의한 loss function을 계산할 수 있기 때문에 순간 기울기 변화율을 이용하는 것이다.
위 그림의 수학자가 만든 미분식으로 W에 대한 loss function의 미분 계수를 사용하면 gradient가 구해진다는 것이다.
그렇게 구해진 gradient를 활용하여 W는 아래의 vanilla gradient descent 방식으로 업데이트되는 것이다.


간단히 설명하자면, 먼저 data input 값, W 값에 대한 loss func의 기울기를 구한다.(analytic gradient)
그 후 기울기(어디로 갱신할 건지)와 step size(얼만큼 갱신할 건지 ex. 보폭)을 기존 W에 더해줌으로써 갱신한다.
이때 - 부호가 앞에 곱해지는 것은 기울기의 반대방향으로 업데이트가 되어야 최적의 방향으로 업데이트되기 때문이다.
단순히 2차 함수 그래프에서 기울기가 음수라면 x가 음의 방향으로 가야 하는 것이 아니라 양의 방향으로 가야 최적점(변곡점)으로 수렴하는 것과 마찬가지다.

그럼에도 gradient를 모든 sample에 대해 계산하는 것은 매우 expensive 하다.
이를 해결하고자 sample을 mini-batch로 나눠 gradient를 업데이트하는 Stochastic Gradient Descent(SGD)가 등장하게 되었다.
일반적으로 32 / 64/ 128 size의 mini-batch를 둔다고 한다.
reference
[1] lecture slides, https://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture3.pdf
'인공지능 > cs231n' 카테고리의 다른 글
| [cs231n] 5강. Convolutional Neural Networks (0) | 2024.06.19 |
|---|---|
| [cs231n] 4강. Backpropagation and Neural Networks (0) | 2024.06.05 |
| [cs231n] 2장. image classification pipeline (0) | 2024.05.24 |


